三角形展开法
出处:按学科分类—工业技术 河南科学技术出版社《钣金技术手册》第442页(3722字)
三角形展开法又称三角线法,是将构件表面依复杂形状分成一组或多组三角形在平面上展开。此法可以用于展开平行线法、放射线法所不能展开的表面成复杂形状的构件,其展开法的基本步骤可表述为:
(1)画出构件的主视图、俯视图和其他必要的辅助图。
(2)作三角形图,求展开实长线,即求出各棱线或辅助线的实长,若构件表面不反映实形,还须求出实形。
(3)按求出的实长线和断面实形作出展开图,在展开图中将各小三角形按主视图和断面图中的顺序和相邻位置依次画出,并将所有有关的点用曲线或折线光滑连接即得展开图。
(一)正四棱锥管的展开
正四棱锥管常用于通风空调管道中,可用三角线法展开,其展开作图如图6-45所示。具体作法如下:

图6-45 正四棱锥管的展开
(1)根据已知的实际尺寸A、B和h作出主视图和俯视图,作辅助线1与3将俯视图梯形分成三角形,再加上棱长2和斜边高4,共有4条辅助线1、2、3、4。
(2)俯视图上4条辅助线为实长线在水平面上的投影,以它们分别为三角形底边。以高度h为高作三角形图,各斜边1′、2′、3′、4′的长度就是实长线长度。
(3)由主视图和俯视图可知下底A与上底B为实长线。先作边A,以A的两端点为圆心,以3′和2为半径画弧,两弧交于c′,作出一个三角形。
(4)用同样的方法可找出b′、a′a、d′和d,连接各对应点,即得展开图。
(二)圆方过渡接管的展开
1.天圆地方管件的展开
图6-46所示的上口圆下口方管件常在通风工程中用做渐变接管。其展开步骤如下:

图6-46 上口圆下口方渐变管件的展开
(1)根据工程所要求的底边长A、圆直径D作俯视图和高度h,作出主视图和俯视图。
(2)等分俯视图圆周为12等份,作1、2、3和4线,其中1与4相等,2与3相等,并向上引投射线至主视图。
(3)作三角形图求出a′与2′、3′、1′、4′的实长。
(4)由于A是实长线,作A线并以O和O1为圆心,求出4″。以O和O1为圆心,以1′、2′与3′线长为半径画弧,从4″点开始,照录断面图中两点之间的弧长与各弧相交,找出3″、2″和1″点。
(5)再以O和O1为圆心,A/2为半径作弧,与以1″为圆心、a′为半径作弧交于5点,光滑连接上口,折线连接下口。检验∠1″5O与∠1″5O1是否直角,若是则展开图正确;否则,上口曲线曲率不对,重新由(4)开始作图。
2.天方地圆管件的展开
如图6-47所示的上口方下口圆管件,既可以是等径也可以是非等径的管件,常用于通风空调工程上,其展开方法与上口圆下口方管件的展开方法完全相同。

图6-47 上口方下口圆管件的展开
3.顶口倾斜上圆下方管件的展开
顶口倾斜上圆下方管件的展开比较复杂,但展开的基本方法不变,仍是三角形展开法(图6-48),其展开步骤如下:
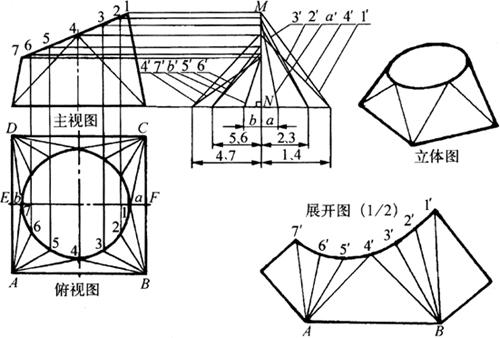
图6-48 顶口倾斜上圆下方管件的展开
(1)作主视图和俯视图:顶圆在俯视图上的投影为一椭圆,可平分顶圆圆周,向主视图引线,找出与顶圆投影线的交点,从而作出主视图和俯视图。
(2)作三角形图:作三角形图时,由于每个三角形底边长需由俯视图上等线长对应移去,而高度由主视图上各线高度引平行线得出,所以在三角形图上,各三角形高度并不一致,这是整体管件展开的关键一步。
(3)其他步骤:以下各步骤按照上口圆下口方管件的展开方法进行。由于顶口倾斜上圆下方管件的顶口不一定是圆,工程上较常见的是椭圆,所以这时各步骤要特别仔细地检验。
4.底面倾斜上圆下方管件的展开
底面倾斜上圆下方管件的展开与上口圆下口方管件相似,仅是底面倾斜。这种管件的底面可以是正方形,也可以是长方形。底面倾斜上圆下方管件的展开图如图6-49所示,其展开步骤如下:
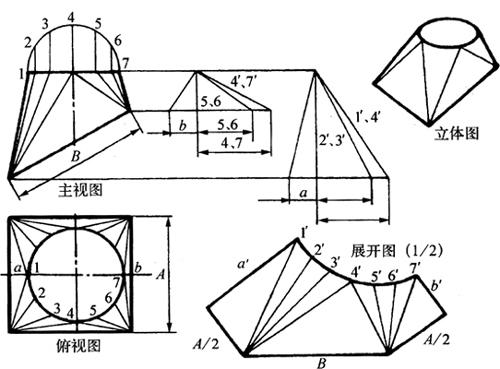
图6-49 底面倾斜上圆下方管件的展开
(1)作视图:根据实际尺寸作主视图,由主视图投影作俯视图,A与B是实长。
(2)作辅助线:先等分顶圆圆周,再在主视图和俯视图上作出各辅助线。
(3)作实线长:由主视图的底线上两个顶点作两个三角形图,分别得出实长线。这一步是展开此管件的关键。
以下各步骤与上口圆下口方管件的展开步骤相同,但检验以下各步骤要更加仔细。
(三)正螺旋面的近似展开
圆柱形螺旋输送机又名搅龙,可用于输送颗粒状、粉末状等物质,也可以作搅拌机构,用途较广。焊在其中心机轴上的螺旋叶片与螺纹一样分单、双线左、右旋,单线螺旋周节等于导程,双线螺旋周节等于1/2导程。螺旋叶片通常按一个导程或稍大于一个导程的螺旋面展开下料,一个螺旋曲面成型后,再在机轴上拼接成连续的螺旋面。
1.三角形展开法
图6-50所示是采用三角形法将螺旋面分成若干三角形面,并将每一个三角形面近似看作平面,求出实形。然后再将这些这些三角形的实形依次拼接在一起,即得的螺旋面展开图。其具体作法如下:
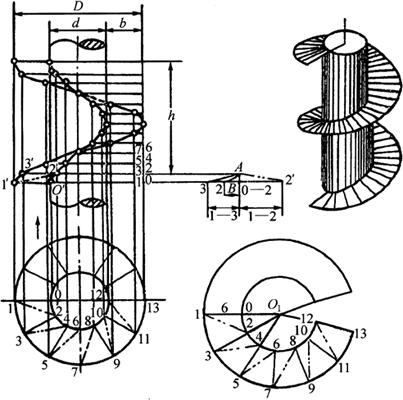
图6-50 正圆柱螺旋面的近似展开
(1)作视图:用螺旋面的内、外直径d、D画出俯视图,十二等分俯视图内、外圆周,等分点分别为0、2、4、…、12和1、3、5、…、13,以点划线和细实线交替连接各点,在主视图取h等于导程,并作十二等分,由等分点引水平线,与俯视图内、外圆等分点所引上垂线得对应交点,区别内、外圆,将各点连成两条螺旋线,完成主视图。
(2)求实长作展开:从主、俯两图上可知,螺旋面上各三角形的细实线边为水平线,其水平投影反映实长,且各线实长相等;各点划线及内、外圆的等分弧为一般位置直线和曲线,投影不反映实长,可用直角三角形法求出(如实长图所示)。求出各线实长后,便可依次作出各三角形实长,完成展开图。
2.简便法展开
由图6-50可知,一个导程的正螺旋面,其展开图为一切口圆环。简便法展开是根据正螺旋面的外径D、内径d和导程h,通过简便计算和作图,求出螺旋面展开图中切口圆环的内、外径和弧长,从而画出展开图。具体作法如下(图5-43):
(1)求实长:用直角三角形法求出内、外螺旋线的实长l及L(图5-43a)。
(2)作梯形:作一直角梯形ABCE,使AB=L/2,CE=l/2,BC=l/2·(D-d),且AB//CE,BC⊥AB。连接AE、BC,并延长两线相交于O(图5-43b)。
(3)作展开:以O点为圆心,OB、OC为半径画同心圆弧,取弧长BF=L,连接FO交内圆弧于G,即得螺旋面的展开图。