同时平衡
出处:按学科分类—数理科学和化学 东北大学出版社《无机物热力学数据手册》第6页(2532字)
在一个多元多相的平衡体系中,可能有几个化学反应同时达到平衡,各相之间也达到平衡。一个化合物很可能同时存在于几个相中,参加几个化学反应。当体系平衡时,此化合物的活度(或分压、浓度等)应符合各反应平衡常数的关系。对于这种复杂体系的热力学计算,首先要确定体系的独立反应数,并选定适当的独立反应。例如含有C,CO,CO2,Fe3O4,Fe,O2等8个物种的体系,可能存在下列8个反应的平衡:
(1) C+O2=CO2
(2) 2C+O2=2CO
(3) 2CO+O2=2CO2
(4) CO2+C=2CO
(5) 3Fe+2O2=Fe3O4
(6) Fe3O4+4C=3Fe+4CO
(7) Fe3O4+2C=3Fe+2CO2
(8) Fe3O4+4CO=3Fe+4CO2
但这8个反应并非都是独立的。这里独立的反应只有3个。例如选取反应(1),(2),(5)作为独立反应,就可以由线性组合推出其它反应:(3)=2(1)-(2);(4)=(2)-(1);(6)=2(2)-(5);(7)=2(1)-(5);(8)=2(3)-(5)。选独立反应的原则是所选反应应包括体系中各物种在内,而且是互相独立的,也就是说,任一独立反应都不能由其它独立反应的线性组合而得到。根据这个原则,上述体系也可以选(2),(3),(5);(1),(3),(6)等作为独立反应。无论哪种选法,其数目都相同(此例是3)。
现假定选取的独立反应是(1),(2),(5),平衡组成只要解此3个反应的平衡关系式就可以求得了:


给定T后,利用本书表2-1的数据,算出这三个反应的△Gθ,再根据式(30)算出各反应的Kθ。反应的△Gθ也可以利用表2-3的△Gθ=A+BT关系式求得。最后联立解式(37)-(39)就可求得pco2,pco,po。。所求得的数值都符合(1)-(8)各式的平衡条件。
对于多元多相体系,应用吉布斯相律求出自由度,对讨论和计算其平衡是有帮助的。相律的一般形式为
f=K-Φ+2 (40)
K=S-R-R′ (41)
式中f——自由度;Φ——相数;K——独立组元数;S——物种数;R——独立化学反应数;R′——浓度的其它限制条件数。R′的意义是不包括在化学平衡和相平衡所要求之内的其它浓度关系数。例如体系NH4Cl以及由其分解所产生的NH3和HC1气体,此两种气体又没有参加其它反应,那么就必然存在%NH3=%HCl的关系,即R′=1。一般复杂体系常常是R′=0。
现将上述复杂体系用相律计算一下自由度。对此体系,S=6,R=3,故K=3。另外,体系有3个固相(C,Fe,Fe3O4)和1个气相,故Φ=4,
f=K-Φ+2=1
这就是说,在T,p总,pco,pco2,po2这些变量中,只有1个是独立的。以其中1个,例如T作为独立变量,其余变量就是它的函数。此独立变量给定后,其余变量就可以计算出来。如果未经自由度的计算,多给了一个条件(例如给定T和p总),则此体系的平衡就不存在,除非有一相消失。
〔计算实例〕 求800K和总压101.325kPa下,H2,H2O(g),CO,CO2,Fe,Fe3O4,C(石墨)的体系平衡时,各气体的分压和百分组成。
此体系可能存在的反应是:
(1) H2+CO2=H2O(g)+CO
(2) C(石墨)+CO2=2CO
(3) Fe3O4+4CO=3Fe+4CO2
(4) Fe3O4+4H2=3Fe+4H2O(g)
(5) Fe3O4+4C(石墨)=3Fe+4CO
(6) Fe3O4+2C(石墨)=3Fe+2CO2
(7) H2+CO=H2O+C(石墨)
(8) 2H2+CO2=2H2O+C(石墨)
此体系有3个独立反应,现取反应(1),(2),(3)作为独立反应。
首先由表2-1查出各物种800K时的G(kJ·mol-1):
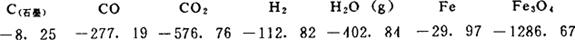
由式(26)计算出反应(1),(2),(5)的△Gθ。
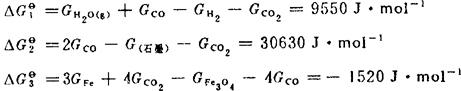
由式(30)计算出Kθ。T以800K代入。
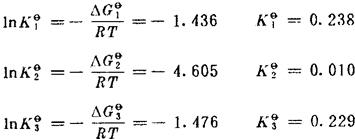
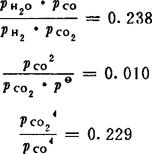
解此3式,可得:
pco=0.701kPa; pco2=0.485kPa;
pH2=85.956kPa; pH2o=14.183kPa;
气相的百分含量:
CO 0.692%; CO20.478%;
H2 84.83%; H2O14.00%;