活塞和活塞杆的计算

出处：按学科分类—工业技术 北京理工大学出版社《新编液压工程手册下册》第1512页（5878字）

结构设计就是确定伺服液压缸的主要特征参数和主要零件的结构形式。它贯穿在设计过程的始终，是决定伺服液压缸实际使用性能的关键。

主要特征参数：有效面积A，缸筒内径D、活塞杆直径d、工作行程S。

(1)有效面积A

有效面积A是一个很重要的参数，其一，在给定供油压力与负载速度条件下，A的大小决定着负载流量，液压油源的功率以及输出力的大小；其二，选择适当的A，可以调整伺服液压缸的时间常数和放大系数以满足系统的动态要求。

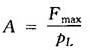
式中 F_max——伺服液压缸要克服的各种负载之和的最大值，称之为最大负载；

p_L——克服负载时两腔的压差，称之为负载压力。

负载力F=F_f+F_m+F_B+F_b

式中 F_f——作用在伺服液压缸上的外力，有恒值外力(例如重力)，按一定规律变化的外力(例如飞机舵面的气动力)，干摩擦力，冲击力，振动力等；

F_m——负载质量与伺服液压缸运动部件的质量，因为加速度产生的惯性力

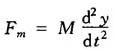
式中 M——负载质量与伺服液压缸运动部件质量之和；

y——负载位移变化，即负载运动方程：

y=y(t)

F_B——阻尼负载力，与伺服液压缸运动速度成正比的负载力。阻尼负载力是粘性阻尼产生的，例如支承滑动面的摩擦力。

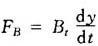
式中 B_t——负载阻尼系数；

F_k——弹性负载力，是与负载位移成正比的力，例如被控对象弹性变形所产生的力；

F_k=K_y

式中 K——负载弹性系数。

于是负载力F为

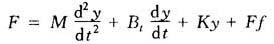
计算有效面积A时应取负载力最大值。

(2)缸径D和活塞杆径d(双活塞杆)

d=mD

式中 m——经验结构系数

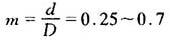
D——缸径，即活塞直径；

d——活塞杆直径。

低速小负载下取小值，反之取大值。于是可按下式确定D与d：

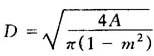
在选定结构系数m时，应考虑下列因素：

·内装位移传感器的，活塞杆是空心的，空心腔孔径d₁应略大于传感器外径，此时杆径d应该按强度来计算。

·铰连处的尺寸要求。

·工艺性与压杆稳定性，尽量避免细长杆。

·材料的品种与规格尽可能市场有售。

·杆径要圆整成标准值(符合GB2348-40给出的系列值)，则有相应的密封件可选用。应尽量避免非标准尺寸。

(3)缸径D和活塞杆径d(单活塞杆)

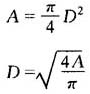
活塞杆直径d通常有两种计算方法：

A．根据速度比的要求

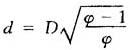
式中 φ——速度比，经验值有2，1．6，1．33，1．25，1．15

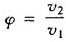
v₁——活塞杆伸出速度；

v₂——活塞杆缩进速度。

表24．7－1 不同速度比下的活塞杆径d

φ值可以根据工作压力的大小来选定

表24．7－2 速度比与工作压力的关系

B．根据强度要求计算活塞杆直径

当活塞杆在稳定状态下，仅承受轴向负载时，杆径d按简单拉、压强度计算，此时

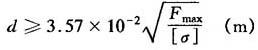
式中 ［σ］——活塞杆材料的许用应力(MPa)。

当活塞杆受到较大弯曲作用时，应按压(或拉)弯联合强度考验，此时：

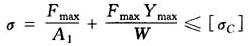
式中 σ——活塞杆应力(Pa)；

F_max——最大负载力(N)；

A₁——活塞杆面积(m²)。对于实心活塞杆则为：

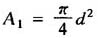
d——活塞杆直径(m)

Y_max——活塞杆断面的抗弯模量(m³)。对于实心活塞杆，则为

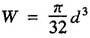
［σ_C］——活塞杆材料的许用应力(Pa)；

σ_s——活塞杆材料的屈服极限(Pa)；

n——安全系数，一般n≥1．4。

计算出d以后，仍要按上述双活塞杆杆径的考虑因素最终确定单活塞杆杆径。

(4)工作行程S

伺服液压缸的工作行程S，主要依据机构的运动要求而定。为了简化工艺和降低成本，应尽量采用GB2349－80中给出的标准系列值，确定工作行程时还应考虑位移传感器的尺寸，与被控对象的连接方式、支承座的固定形式即未端条件。

(5)不受偏心载荷活塞杆稳定性的计算

伺服液压缸主要零部件的强度计算基本上和液压缸相同，可以参照23．3节液压缸主要零部件设计。这里着重介绍活塞杆的纵向弯曲强度计算。

伺服液压缸在受到轴向压缩负载力作用的情况，如图24．7－1所示。倘若活塞杆直径d与伺服液压缸的安装长度l之比l／d≥10时，就不能按单纯的压缩状态处理了，必须将伺服液压缸整体作为一种细长杆来处理，由材料力学可知，受压细长杆，当负载力接近某一临界值时，杆将产生纵向弯曲，且其挠度值随着压缩负载力的增加急剧增大，以至产生屈曲破坏，失去稳定性。

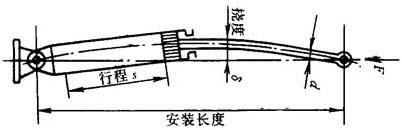
图24．7－1 承受压缩负载的同服液压缸

对于没有偏心载荷的细长杆，其纵向弯曲强度的临界值，可按等截面法和非等截面法计算。

A．等截面计算法

当细长比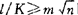时，可按欧拉公式计算临界载荷P_K。此时

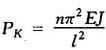
式中 PK——活塞杆纵向弯曲破坏的临界载荷(N)；

n——末端条件系数，见表24．7－3；

表24．7－3 末端条件系数

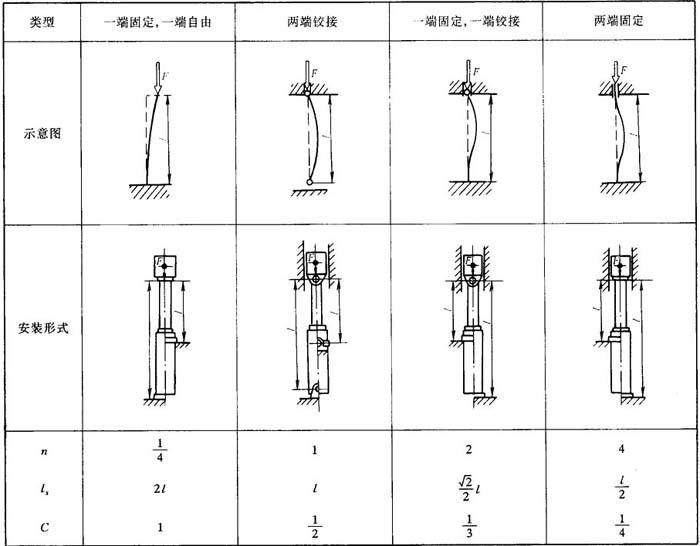
E——活塞杆材料的弹性模量(Pa)；

J——活塞杆截面的转动惯量(m⁴)实心活塞杆：

空心活塞杆：

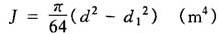
d——活塞杆外直径(m)；

d₁——空心活塞杆内径(m)；

l——伺服液压缸的安装长度，即活塞杆全伸出时，活塞杆端支点和伺服液压缸支承座间的距离(m)；

K——活塞杆断面的回转半径(m)实心活塞杆：

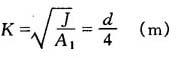
空心活塞杆：

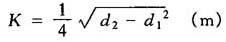
A₁——活塞杆截面积(m²)

实心活塞杆：

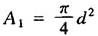
空心活塞杆：

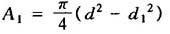
m——柔性系数，为实验常数，见表24．7－3。

若活塞杆为实心杆，且用钢铁材料制造的，临界载荷P_K可简化为

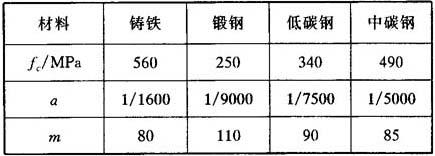
表24．7－4 实验常数f_c，a，m

当活塞杆细长比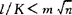时，用戈登-兰金公式计算临界载荷P_K，此时：

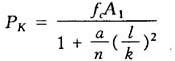
式中 f_c——材料强度实验值(MPa)；

A₁——活塞杆截面积(m²)；

a——实验常数，见表24．7－3；

m——柔性系数，见表24．7－3，这里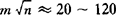

当活塞杆细长比l／K<20时，可按纯压缩计算。

B．非等截面计算法

等截面计算法是把缸筒的惯性矩看成与活塞杆的相同，这与实际情况差别较大，因而等截面计算法得到的P_K值较为保守。采用非等截面法计算得到的P_K值，与实际情况较接近。其计算公式为：

式中 k——形状系数，由图24．7－2或图24．7－3查出

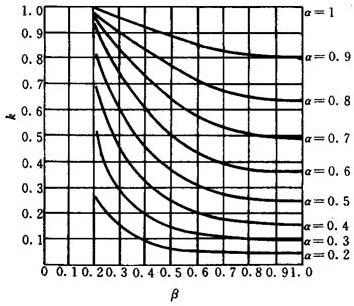
图24．7－2 形状系数(α曲线图)

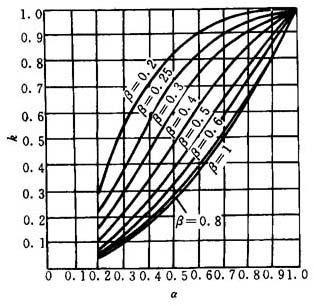
图24．7－3 形状系数(β曲线图)

图中

J₁——活塞杆的转动惯量(m⁴)；

J₂——缸筒的转动惯量(m⁴)；

l₁——活塞杆的伸出长度(m)；

l——伺服液压缸的安装长度(m)。

为了保证活塞杆不产生纵向弯曲，活塞杆实际承受的压缩负载力要远小于临界载荷P_K，即

式中 F_max——活塞所承受的最大压缩负载力(N)；

P_K——临界载荷(N)；

n_K——安全系数，n_K=2～4。

(6)承受偏心载荷时活塞杆稳定性的计算

伺服液压缸由于结构或安装铰链的原因，活塞杆往往承受一定的偏心负载，此时的临界载荷应按下式计算：

式中 P_K——临界载荷(N)；

σ_s——活塞杆材料的屈服极限(Pa)；

A₁——活塞杆截面积(m²)；

e——截荷偏心量(m)；

d——活塞杆直径(m)；

θ——挠度

C——系数，见表24．7－1；

E——活塞杆材料的弹性模量(Pa)；

l——活塞杆的计算长度，即伺服液压缸的安装长度(m)；

K——活塞杆断面的回转半径(m)。