二阶系统频率特性与过渡过程的关系

出处：按学科分类—工业技术 北京理工大学出版社《新编液压工程手册上册》第153页（2523字）

(1)闭环幅频特性与过渡过程的关系

A．闭环频域指标

若系统闭环频率特性为

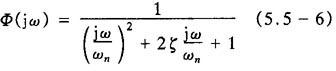
闭环幅频特性为

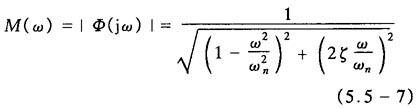
当0＜ζ＜1时，M(ω)曲线的一般形状示于图5．5－11。对照图5．5－11给出表示M(ω)形状的特征参数如下：

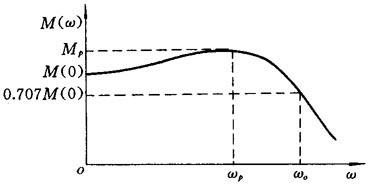
图5．5－11 二阶系统的闭环幅频特性

·闭环幅频特性峰值M_p：它是闭环系统幅频特性的最大值。

·峰值频率ω_p：是闭环系统幅频特性出现峰值时的频率值。

·带宽和带宽频率：若ω从零增加到ω₀时，M(ω₀)下降为M(0)的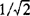倍，即

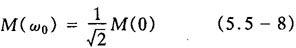
则零至ω₀的频率范围称为系统的带宽(或称通频带)，ω₀称带宽频率。

M_p，ω_p，ω₀表示了闭环系统幅频特性的主要特征，它们和过渡过程关系最密切，通常把这三个参数称为过渡过程的闭环频域指标。

B．M_p，ω_p，ω₀与ζ、ω_n之间的关系

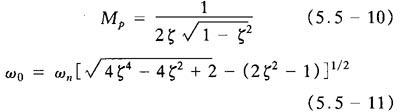
C．时域指标与频域指标的关系

对式(5．5－10)和表5．4－3给出的超调量表示式分别给以不同的ζ值，则得一组M_p和σ_p，列于表5．5－3。

表5．5－3 二阶系统ζ，M_p，σ_p的对应值

根据表5．5－3中的数据，画出σ_p随M_p变化的关系曲线示于图5．5－12。曲线表明：M_p增大，σ_p也随之增大。如果给定M_p，可根据曲线查出σ_p的数值，例如M_p=1．36，对应σ_p=25．3%。

图5．5－12 σ_p与M_p之间的关系曲线

对于式(5．5－9)和式(5．5－11)分别给以不同的ζ值，计算ω_p／ω_n和ω₀／ω_n的数值，列于表5．5－4。

表5．5－4 二阶系统ζ和ω_p／ω_n，ω₀／ω_n的对应值

根据表5．5－4的数据，画出ω_p／ω_n，ω₀／ω_n随ζ变化的曲线示于图5．5－13。

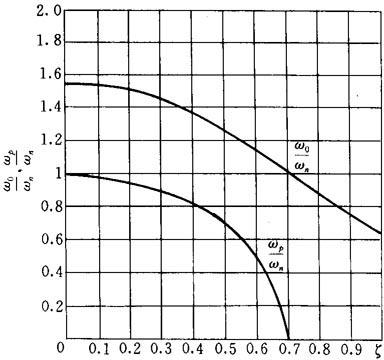
图5．5－13 ω_p／ω_n，ω₀／ω_n与ζ的关系曲线

从图5．5－13可以看出：

·当ζ比较小时，如ζ＜0．4，可视为ω_p／ω_n≈1，即ω_p≈ω_n。

·当ζ=0．707时，ω₀／ω_n=1，即ω₀=ω_n；在ζ=0．707附近，如0．5≤ζ≤0．8区间，可视为ω₀≈ω_n。

由上面特点可知，在计算时域指标t_r和t_s时，在ζ＜0．4范围内，可用频域的ω_p近似代替时域的ω_n；在0．5≤ζ≤0．8范围内，可用频域的ω₀近似代替时域的ω_n。一般希望闭环系统工作在ζ=0．707附近，所以用ω₀代替ω_n比用ω_p代替ω_n更准确些。

(2)开环频率特性与过渡过程的关系

A．开环频域指标

在分析闭环系统动态特性时，常用开环频率特性的两个特征量，即截止频率ω_c和相角裕量γ来表征系统的过渡过程特征，并称其为开环频域指标。

B．γ，ω_c与ζ，ω_n的关系

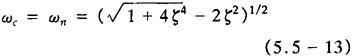
C．过渡过程时域指标和开环频域指标的关系

σ_p与γ之间的关系 根据式(5．5－12)和表5．4－3中σ_p的表达式计算出不同ζ值的γ和σ_p，计算结果列于表5．5－5。

表5．5－5 γ，σ_p与ζ的对应值

根据表5．5－5给出以ζ为参变量σ_p随γ的变化曲线示于图5．5－14。如果知道系统的相角裕量γ，可从图5．5－14所示曲线查出相应的σ_p值。例如，γ=44°，可查得σ_p=25．4%。

ts与ω_c的关系 典型二阶系统的调节时间(△=±5%)为

将式(5．5－13)代入上式，得

(5．5－14)

由式(5．5－12)和式(5．5－14)可得

(5．5－15)

图5．5－15给出了t_sω_c与γ的关系曲线。如果系统的相角裕量γ，即σ_p已经给定，则t_s与ω_c成反比。ω_c越大，系统的调节时间越短。

图5．5－14 σ_p－γ关系曲线

图5．5－15 二阶系统的t_sω_c－γ曲线