科学史话
出处：按学科分类—社会科学总论 中国建材工业出版社《中国文书大典中卷》第950页（2700字）
【简介】：
用平铺直叙的手法向读者介绍某一学科发展变化的历史，往往枯燥无味，读者难以接受，难以记忆。为了使读者乐于接受，而且对某项科技史发生兴趣，可以采用“史话”的形式，即用讲故事或谈家常的方式来讲述某一学科的发展史、科学和技术的发现史和发明史、人类认识和征服自然的历史、大自然本身的演化史等。撰写科技史话，作者首先要对写作题材掌握大量的史料，掌握驾驭时空跨度大的文字能力，还要运用大量有趣的、有血有肉的故事情节，描写“历史”。使某一学科的“漫长”历史缩小或涌现在读者眼前，栩栩如生，兴味盎然，语言也要明快、幽默、有趣。如美国科普作家房龙的《人类的故事》、《发明史话》，苏联科普作家伊林的《黑白》、《十万个为什么》等，都是闻名世界的史话形式的知识性科普作品。近年来，我国也有一些不同风格的史话形式的作品问世。如刘仁庆的《中国古代造纸史话》、郭正谊的《太阳元素的发现》等。
史话形式的作品不仅介绍了具体的科学知识，还能传播科学的思想方法和实验方法等。对正在学习的青少年，补充了课堂学习的不足，提高他们对科学的兴趣；对教师则可以丰富其讲课内容；对一般读者，也是一种科学史、辩证唯物主义和历史唯物主义的宣传教育。
【范例】：
漫话圆周率 (科学史话)
茅以升
圆周率是个什么东西?少年朋友们大概都知道，它就是一个圆的“圆周”长度和它的“直径”长度相比的倍数。不论圆的大小如何，这个倍数都是一样的，因而是一个“常数”，也就是一个不变的数，在数学上名为“π”。它是希腊文“周围”的第一个字母。在自然科学里，圆周率π这个数值，用途非常之广，同时也是一个非常奇特的数值。在数学里，可以同它相比的，还有两个奇特的数值，一个是“自然对数”的“底”，名为“e”；另一个是“负一”的平方根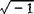
，名为“虚数i”。再加上两数学里最重要的数值，一个是“1”，一个是“0”，这五个数值联成一个极简单的关系式：eπi+1=0。可见，数学是多么引人入胜呵!
圆周率π的数值，该是多少呢?为了求这个数值，自古以来不知有多少数学家绞尽脑汁，算出了一个比一个更精确的值。起初以为可以算到底，求出π值的全值。但是算来算去，越算越没有个完，始终到不了底，直到16世纪中叶，才有个法国数学家费托，用数学证明π是个“无尽数”，按一定法则，可以无止无休地算下去，不象分数，如1／3，虽然也“无尽”，但却简单。现在来回溯一下，我国和外国的数学家对这圆周率π的数值的贡献。
我国在很早的时候，就有“周三径一”之说，即π=3，在公元前100年的一部《周髀算经》里，就有记载。后来慢慢知道，圆周率应当比3略大一点，就是说，在整数3的后面应当还有小数，到了东汉时，我国天文学家、数学家张衡(公元78～139年)，提出了一个很妙的数值，说圆周率等于10的平方根，即π=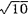
=3．16。这个数值很简便，容易记得住，就是到了现代，有时也还用到它。这个数值，在将近500年后，才在印度发现。三国时，魏国的数学家刘徽，在公元263年提出一个更准确的圆周率值：π=
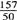=3．14，并且发表了他的计算方法，称为“割圆术”，是数学上的一个贡献。在刘徽的前后，还有很多数学家提出了各种不同的圆周率。
最辉煌的成就，要算南齐时祖冲之(公元429～500年)的圆周率值。他用一种方法叫做“缀术”，得出π值在3．1415926和3．1415927之间，无一字错误，是世界上最早的七位小数精确值。他又提出两个分数值，一个叫“约率”，π=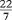
=3．14；另一个叫“密率”，π=
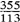=3．1415929。“约率”和希腊的阿基米德的圆周率值相同，但“密率”在欧洲是米切斯于公元1527年才发表的，比我国晚了1000多年，这真是祖国的光荣。现在月球背面的一个山谷，就命名为“祖冲之”，可见国际上对他的景仰。这个“密率”很容易记住，先把三对相连的奇数，排成一行，即113355，然后在当中一分，前面的113就是分母，后面的355就是分子。如用四位数以下的分数，来表达圆周率值，那就不可能得到比“祖率”更准确的了。
15世纪以后，欧洲科学蓬勃兴起，所谓“方圆学者”(求同一面积的一方一圆)，日见增多，于是圆周率值也越算越精确，大家都以算出的π的小数位数越多越可贵。最突出的要算德国的卢多夫(公元1540～1610年)，竟将π值的小数位数算到35位，而且经过其他学者核对，无一字之差。他感到不虚此生，遗嘱将这35位值，刻在他的墓碑上。有的德国人至今还把圆周率值称为“卢氏值”。
后来，求圆周率的方法日有进步，小数位数增加很快到公元1706年时，达到100位，1842年时达到200位，1854年时达到400位，最后到1873年时竟达到707位!算出这个数的英国数学家山克司，可算在这场圆周率计算的竞赛中得到冠军，因为以后再没有人用手算来和他较量了。山克司用了15年工夫才算出这707位值，但是很可惜，经过后来校对，其中只有530位小数是准确的。
在这里，读者一定会问，在有了电子计算机以后，这个圆周率竞赛，该没有什么意义了吧!诚然，利用电子计算机，π的小数位数的增长速度，确是惊人!先是有人在一天一夜里算出2048位，后来在1967年有两位法国人，一个叫纪劳德，另一个叫狄山姆，竟然把小数位数增加到50万位!如果把这50万位小数都在这里报告出来，这本《少年科学》全本都印不完。想了个折中办法，把这50万位的头100位，和末了的499991～500000的10位，在这里记下来。
π=3．14159 26535 89793 23846 26433
83279 50288 41971 69399 37510 58209
74944 59230 78164 06286 20899 86280
34825 3421 1 70679 … … … 51381
95242
请读者看一看并且试一试，能对这许多数字，在脑筋里记牢多少位。我年轻时曾对圆周率问题发生很大兴趣，把前面的一百位都记住了，到现在还记得住。