3.光学平行度与棱镜几何误差的关系
出处:按学科分类—工业技术 北京理工大学出版社《光学设计手册修订版》第199页(2183字)
3.1 术语定义
(1)工作面——棱镜中,凡起折射和反射作用的抛光平面,都叫做工作面。其余的毛面,就叫做非工作面。
(2)棱——两个相邻工作面的交线。
(3)棱差——棱镜的棱的实际位置对理论位置的偏差,(以夹角表示)叫做棱差。棱差分为两类,即A棱差及C棱差。
4棱差——平面棱镜的任一工作面(屋脊面除外)与其所对的棱的平行度。A棱差又称为面棱棱差,以符号γA表示。
C棱差——屋脊棱镜的屋脊棱在垂直于屋脊平分面的平面内,相对于理论位置的倾转角度。C棱差又称屋脊棱差,以符号yC表示。
(4)反射面的光轴入射角——光轴经棱镜的反射面反射时,光轴与反射面法线的夹角,以符号i表示。见图3-4。
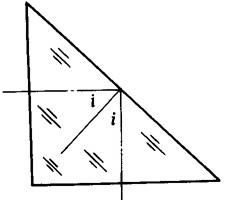
图3-4 反射面光轴入射角
(5)屋脊的光轴入射角——屋脊棱镜的光轴经屋脊反射时,光轴与屋脊平分面内垂直于屋脊棱的准法线的夹角,以符号β表示,见图3-5。
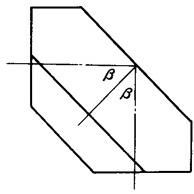
图3-5 屋脊的光轴入射角
3.2 光学平行度的影响
首先是白光光束通过棱镜后产生色散,此外,成像用的平面棱镜的第一光学平行度会导致光轴偏,第二光学平行度会导致光轴偏和像倾斜。
对于空间棱镜和其他复杂棱镜的影响,可以分析为两个或两个以上平面棱镜看综合效果。
3.3 第一光学平行度
它是由平面棱镜在光轴截面上的角度误差引起的。两者之间的关系,只要将棱镜展开为等效平板时即可找出。
例如图3-6中一个弦面反射的直角棱镜ABC展开为等效平板后,ABC′为直角棱镜ABC经弦面AB反射后所成的像。理论上,AC与C′B应该平行。若不平行,则AC与C′B的夹角就是这个棱镜的第一光学平行度。第一光学平行度是内错角∠CAB与∠ABC′之差。∠CAB与∠ABC′的名义值都是45°,这两个角度之差用符号δ45°表示。因此,弦面反射的直角棱镜的第一光学平行度与角度误差的关系式是:
δ1=δ45°
以后用符号△表示某一角度的实际值与名义值之差,例如直角面反射的直角棱镜有:
θⅠ=2△90°
对于有两个反射面的棱镜,光线经过这两个面反射后的偏转角等于两个反射面夹角的两倍。两个折射面的夹角,必须与之适应,才能保证第一光学平行度为零。

图3-6 棱镜的展开
3.4 第二光学平行度
是由平面棱镜的棱差引起的
(1)若在平面棱镜中某一反射面与其所对的棱所构成的棱差为γA,则它所引起该棱镜的第二光学平行度等于该反射面的光轴入射角i的余弦的两倍再乘上γA,即
θⅠ=2γAcosi
若在平面棱镜中某一折射面与其所对的棱的棱差为γA,则它所引起的该棱镜的第二光学平行度就等于γA,即
θⅠ=γA
若在带屋脊的平面棱镜中,屋脊棱的棱差为γC,则它所引起的该棱镜的第二光学平行度等于该屋脊的光轴入射角β的正弦的两倍再乘上yc,即
θⅠ=2γCsinβ
(2)对于平面棱镜,主要用反射面、折射面和折反射面(一个工作面同时起折射和反射作用),来区别选用不同的基准棱。其符号为:
γA(反)-反射面与它所对的棱构成的A棱差。
γA(折)-折射面与它所对的棱构成的A棱差。
γA(折反)-折反射面与它所对的棱构成的A棱差。
为了便于用修改非屋脊的工作面来改正屋脊棱的θⅠ,可以把屋脊看作一个反射面(通过屋脊棱且与屋脊平分面垂直)与其相邻的工作面相交,得到一个假想的基准棱来计算其所对的工作面的γA。
若有四个或四个以上工作面(屋脊可以看作一个工作面)的平面棱镜,固定一个基准棱后,其所对的两个或两个以上工作面产生的γA有互相叠加或抵消作用。修改时,可以只改一个工作面,在满足其它要求时,也可以同时修改两个面。