程序编制中的数学处理
出处:按学科分类—工业技术 北京出版社《现代综合机械设计手册下》第2954页(18948字)
6.5.1 数学处理的内容
数学处理的内容包括:
①基点和节点的计算。组成零件轮廓线的各个几何元素间的联接点称为基点,如两直线的交点,直线与圆弧的交点或切点,圆弧与二次曲线的交点或切点等。按数控系统插补功能的要求,在满足允许程序编制误差的条件下,对零件轮廓曲线进行分割得到的各分割点称为节点,如用直线逼近零件轮廓时,相邻两直线的交点即为节点;用圆弧逼近零件轮廓时,相邻两圆弧的交点或切点即为节点。基点和节点数据是数控系统输入信息的原始数据。
②刀具中心轨迹的计算。零件加工程序是用刀具上确定点(刀位点)的运动轨迹来描述的。刀位点也称为刀具中心。数控系统从对刀点开始控制刀具中心走出直线或圆弧,但所要求的零件轮廓是由刀具的切削部分加工出来的,所以需要进行刀具偏移计算。在有刀具偏移运算功能的数控系统中,程序编制中只要算出零件轮廓的基点和节点数据,给出有关刀具补偿指令和相应数据,数控系统便可算出刀具偏量,得到刀具中心轨迹。若数控系统不带有刀具偏移运算功能,则需算出与零件轮廓的基点和节点相对应的刀具中心轨迹上的基点和节点坐标值,得到刀具中心轨迹。
③辅助程序段的数值计算。包括从对刀点到切入点(刀具开始与零件轮廓接触的点)的切入程序及切削完了返回到对刀点的返回程序所需数据的计算。对于增量坐标的数控系统,需要进行增量值的计算,如直线终点相对其起点的坐标增量计算,圆弧终点相对其起点的坐标增量的计算及圆弧圆心相对起点的坐标增量计算等。对于绝对坐标的数控系统,一般不进行增量值计算,直线终点、圆弧终点的坐标值都直接给出。但圆弧的起点仍用其相对圆心的坐标值给出,或圆心相对圆弧起点的坐标值给出。
此外,还有脉冲数计算。这是指将数值计算得到的毫米数(线位移)或度数(角位移)换算为脉冲数的计算。
6.5.2 直线、圆弧轮廓零件的数值计算
直线、圆弧轮廓零件数值计算中的一项主要内容,是基点的计算。这类零件基点的形成归纳起来有以下五种方式:直线与直线相交;直线与圆弧相交;直线与圆弧相切;圆弧与圆弧相交;圆弧与圆弧相切。直线和圆弧的标准方程分别为:
Ax+By+C=0
(x-ξ)2+(y-η)2=R
通过求联立方程组的解,即可得到基点的坐标。形成基点的五种形式及基点的计算公式见表8.5-70,表中还给出刀具中心轨迹上的基点计算公式。刀具中心轨迹即零件轮廓的等距线,直线Ax+By+C=0的等距线方程为Ax+By+C=±l 。
。
表8.5-70 直线、圆弧轮廓零件基点的计算公式



当原始方程中B≥0时(B=0时,A<0),对于相同的x值,等距线上的y值大于原直线的y值时取正,反之取负;若直线平行于y轴,则等距线上的x值大于原直线的x值时取正,反之取负。如果原始方程中B<0时,符号的选取方法与上述相反。
圆(x-ξ)2+(y-η)2=R2的等距圆方程为(x-ξ)2+(y-η)2=(R±τ)2。等距圆在原始圆凸侧时,式中符号取正,反之取负。
由实际生产的零件可归纳出11种直线定义方式和14种圆弧定义方式,见表8.5-71和8.5-72。由表8.5-71得到直线方程截距式y=Kx+b的参数k和b,也就得到直线一般方程式Ax+By+C=0的参数A(=-K)、B(=1)、C(=-b),由表8.5-72得到标准的圆方程式(x-ξ)2+(y-η)2=R的参数ξ、η和R,进而可按表8.5-70的公式进行基点的计算。
表8.5-71 截矩式直线方程K、b参数的计算




表8.5-72 标准圆方程参数ζ、η、R的计算





6.5.3 非圆曲线轮廓零件的数值计算
非圆曲线指的是椭圆、双曲线、抛物线、一般二次曲线、阿基米德螺线、对数螺线、摆线和渐开线等。这类曲线轮廓零件的数值计算包括:根据允许的插补误差和数控系统具有的插补方式计算各插补段的起点和终点坐标。若数控系统无刀具偏移运算功能,则还需进行刀具中心轨迹坐标的计算。
用直线逼近曲线的数值计算有三种方法:
①等插补段法。这种方法是使各插补段的长度相等。由于零件轮廓曲线的曲率各处不等,因此各插补段的程编误差也各不相等,必须使最大插补误差δmax小于允许的插补误差δ允,才能满足程序编制的精度要求。在用直线逼近曲线时,通常假设最大误差出现在曲线半径最小处,并沿曲线法线方向计量(这一假设适用于大多数情况)。其算法的计算过程是:零件轮廓曲线的原始方程为y=f(x),其曲率半径为

将R对x求一阶导数并令其等于“0”( =0)得
=0)得

由此式求得x,代入R表达式求得Rm1n。如图8.5-147所示,以Rmi0为半径作圆,在允许的插补误差δ允时的弦长ab为ab=2 或ab≈2
或ab≈2 (8.5-133)
(8.5-133)
以曲线的起点(x0,y0)开始,以(x0,y0)为圆心,ab为半径作圆:
(x-x0)2+(y-y0)2=8Rmimδ允 (8.5-134)
求其与y=f(x)的交点,得x1,y1,此点即为节点。再以此点为圆心、ab为半径作圆,求出其余各节点的坐标值。

图8.5-147 等插补段长度的确定
②等插补误差法。这种方法的特点是使各插补段的插补误差相等,并且小于或等于允许的插补误差。显然,用这种方法确定的各插补段的长度是不相等的。采用这种方法得到的插补段数较前一种方法少,因此对于大型或形状复杂的零件更具有意义。等插补误差法又称为平行线法,其具体过程如图8.5-148所示,以(x0,y0)为圆心,δ允为半径作圆:

图8.5-148 等插补误差法原理
(x-x0)2+(y-y0)2= (8.5-135)
(8.5-135)
求此圆与零件轮廓曲线y=f(x)的公切线:


式中的y=F(x)表示圆的方程。解以上联立方程组,得到 、
、 、
、 、
、 进而得到K。过(x0,y0)点,作斜率为K的直线:
进而得到K。过(x0,y0)点,作斜率为K的直线:
y0-y0=K(x-x0)
求y=f(x)与y=K(x-x0)+y0的交点(x1,y1)。再从(x1,y1)点开始重复上述计算,求其余各节点。
③等间距法。这种方法的特点是使每个插补段的一个坐标增量相等。如在直角坐标系中,使插补段的x坐标增量或y坐标增量相等;在极坐标系中,使转角坐标增量或向径坐标增量相等。采用这种方法的过程是:对于零件轮廓曲线y=f(x),首先根据零件加工精度的要求,由经验选取x坐标增量Δx。然后由起点开始,每增加-个Δx,代入y=f(x)求出另一坐标值。这种方法需要验算,其误差的最大值必须小于或等于δ允。对于比较平滑的曲线,应验算两节点间距离最大处的误差。对于曲率变化比较大的曲线,应对曲率变化较大的段的误差进行验算。如果有曲线拐点,还应对该处的误差进行验算。验算方法如图8.5-149所示。过验算段PQ两端点P和Q的直线方程为


图8.5-149 误差验算图示
距该直线为δ允的直线方程为
Ax+By=C±δ允 (8.5-140)
(8.5-140)
式中 A=yP-yQ; B=xQ-xP; C=xP(yp-yQ)-yP(xP-xQ)。

若有两个以上解,且解在P、Q之间(图8.5-149中的a),则表示超差,应缩小间距,并重新验算,直至满足要求为止。若有一解、无解(图8.5-149中的b)或虽有两个以上解,但在P、Q点之外,则表示不超差。
刀具中心轨迹节点的计算:如图8.5-150所示。过零件轮廓相邻两节点作直线

图8.5-150 刀具中心轨迹节点计算

将上式变为一般形式
Anx+Bny+Cn=0
式中 An=yn-1-yn;Bn=xn-xn-1;
Cn=xn-1yn-yn-1xn,
求距直线为,的直线
Anx+Bny+Cn=±,
解联立方程

(8.5-142)
得交点(xm,ym)后,重复上述计算,便可得到各刀具中心轨迹节点的坐标值。
在用圆弧逼近曲线的数值计算中,用彼此相交的圆弧逼近曲线有三点作圆法和圆弧分割法。其中,三点作圆法是先用直线逼近曲线,然后再通过连续三点作圆弧。图8.5-151所示是直线逼近和圆弧逼近误差的关系。δ1为用直线逼近曲线的误差,δ2为用圆弧逼近曲线的误差。由直线与y=f(x)曲线得

式中的Ra为y=f(x)曲线在A点的曲率半径。
由直线和圆弧得

式中的R为过A、B、C三点的圆的半径。由此可得

若使圆弧与y=f(x)曲线间的误差δ2=δ允,则


图8.5-151 直线、圆弧逼近误差的关系
具体的计算步骤如下:
计算用直线逼近y=f(x)曲线的节点,得A、B,C……各点(参见图8.5-151)。程编误差δ1=δ允。
通过连续三点(x1、y1)、(x2、y2)、(x3、y3)作圆:
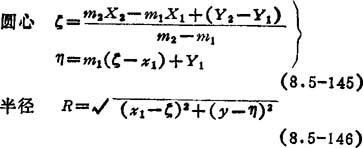
式中 X1=(x1+x2)/2;y1=(y1+y2)/2;X2=(x2+x3)/2;y2=(y2+y3)/2;m1=(x2-x1)/(y2-y1);m2=(x3-x2)/(y3-y2)。
按以下公式计算连续三点的曲率半径RA、RB、Rc,并取其平均值RP:

依给出的δ允,计算δ值;

以δ为程编误差,计算用直线逼近y=f(x)曲线的各个节点,得A、B、C…。然后过连续三点作圆,计算新圆心和半径(ξ1、η1、R1)。ξ1、η1和R1即为所求的值。最后,验算圆弧逼近误差:

若δ1≤δ允,则满足要求,否则应减小δ值。
图8.5-152所示为圆弧分割法,这种方法适用于单调曲线。如果不是单调曲线,则需在曲线的拐点和凸点处分段,使每段曲线为单调曲线。圆弧分割法计算节点的步骤是,先从曲线起点(xn,yn)开始作圆弧:

图8.5-152 圆弧分割法示意图

得交点xn+1,yn+1,并重复上述计算,得到其余各节点。
解联立方程

解联立方程

得刀具中心轨迹节点(xm+1,ym+1)。凸轮廓曲线,式中取正号;凹轮廓曲线,式中取负号。重复计算,即可得到刀具中心轨迹的其余各节点坐标值。
在用圆弧逼近曲线的数值计算中,也用彼此相切的圆弧逼近曲线。这种方法的特点是,圆弧间的连接是光滑的。如图8.5-153所示,过曲线y=f(x)上的四点A、B、C、D作曲线的法线,其中A、B点法线相交于M,C、D点法线相交于N。以M点为圆心,AM为半径作圆M。以N点为圆心,DN为半径作圆N。当M圆和N圆的半径之差等于其中心距时,M圆和N圆彼此相切。y=f(x)曲线与M圆和N圆间的最大误差分别发生在B点和C点(两曲线相交,且交点间两曲线无拐点和凸点,则其间最大距离发生在两曲线斜率相等处)。当满足|AM-BM|≤δ允、|DN-CN|≤δ允时,逼近圆弧M和N与y=f(x)之间的误差小于允许值δ允。由于在起点A和终点D处M圆和N圆与曲线y=f(x)相切,因此相邻两计算单元的圆弧也彼此相切,从而保证整个逼近圆弧是连续的。其计算方法如下:

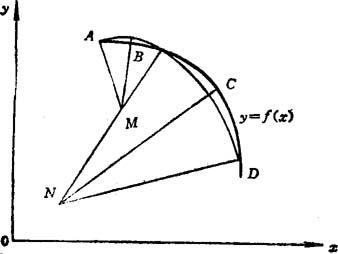
图8.5-153 彼此相切圆弧逼近曲线原理
从起点A开始,任意选取三点B、C、D,A、B两点的法线方程如下

解联立方程得到M点坐标

由C、D两点的法线方程可求出N点坐标

用迭代法解下面的联立方程,求B、C、D坐标值:
式中 yA=f(xA);yc=f(xC);yD=f(xv)。
最后求出圆弧圆心M、N,半径RM、RN及切点G。应当指出,只有曲线有连续的一阶导数,才能用彼此相切圆弧进行逼近。若曲线有断裂点,应以断裂点作为分割节点。如果曲线有拐点和凸点,则应将拐点和凸点作为计算单元(每一计算单元为四个点)的分割点。
为正常凸点;
当 =0,
=0, =0时为异常凸点。
=0时为异常凸点。
式中的θ角为曲线的切线与x轴的夹角。
6.5.4 列表曲线轮廓零件的数值计算
对于列表曲线轮廓的一般处理方法是:先找出描述列表曲线的数学表达式(即第一次逼近),再根据精度要求采用直线或圆弧进行逼近(即第二次逼近)。
用来描述列表曲线的数学表达式应满足:方程式表示的零件轮廓应通过给出点(型值点);方程式表示的零件轮廓应与由型值点给出的轮廓凸凹性一致;当用多个参数不同的同样方程描述列表曲线时,在连接点处应有连续的一阶导数或二阶导数,在没有连续的一阶导数时,其连接点处两边的导数差值应尽量小。常用的数值计算有牛顿插值法和样条函数法。
如果列表曲线的型值点有(x0、y0)、(x1,y1)、…(xn,yn)共n+1个点,则牛顿插值多项式为:
Pn(x)=f(x0)+f(x0,x1)(x-x0)+…+f(x0,x1,…xn)(x-x0)(x-x1)…(x-xn-1) (8.5-157)
这是次数不超过n的多项式,式中

f(x0,x1)、f(x0,x1,x2)、f(x0,x1,…xn)分别称为一阶、二阶和n阶均差(或差商)。
在数控编程中,多数采用牛顿插值多项式的前三项,即通过三个型值点的二次插值三项式
y=f(xi-1)+f(xi-1,xt)(x-xt-1)+f(xi-1,xt,xi+1)(x-xi-1)(x-xi) (8.5-158)
式中 i=1,2,…n。令

式中 i=0,1,2,…n。则上式可写成
y=B1x2+(A1-B1xi-1-B1xi)x+(B1xl-1xt
A1xi-1+yi-1) (8.5-159)
显然,上式为一族具有垂直轴的抛物线,如图8.5- 154所示。根据插值多项式的误差分析,在xi-1、xt、xt+1三点的二次插值式中,区间〔xt-1,xi〕内插值误差最小,因此程编时加密点应在区间〔xt-1,xt〕间给出,即〔x0,x1〕用P0,1,2(x)抛物线描述;〔x1,x2〕用P0,1,2(x)抛物线描述;〔xj-1,xt〕用Pj-2,t-1,j(x)抛物线描述。通过三个型值点用牛顿二次插值三项式描述两点间的曲线形状,可以保证型值点两边的导数差较小,特别是对型值点较平滑的情况,其导数差甚小。列表点对坐标轴等间距时(这种情况是很多的),采用牛顿等距插值公式更为方便。对于图8.5-155所示的x轴等距分布的列表曲线,用下式描述区间〔xt-1,xt〕的曲线形状:

图8.5-154 具有垂直轴的抛物线族

图8.5-155 x轴等距分布列表曲线

式中 Δyi-1=yi-yj-1;Δyl=yl+1-yj;Δ2yi-1=Δyi-Δyj-1=yj-1+yt+1-2yi。上式是二次抛物线。称为牛顿二次前插公式。对于最后两点的区间〔xn-1,xn〕,用牛顿后插公式描述;

式中 Vyn=yn-ym-1;▽yn-1=yn-1-yn-2;▽2yn=Vyn-▽ym-1。Vyn称向后差分,Δyl相应称为向前差分。
对于直线(圆弧)插补逼近牛顿二次三项式,如图8.5-156所示,这是根据插补误差定步长的近似等插补误差法的一种插补方法。过Pt点作抛物线y=Ax2+Bx+C的切线,其方程为
y=(2Axt+B)(x-xt)+yj
或 y=(2Axj+B)x-Axj2+C

图8.5-156 根据插补误差定步长法示意图
在Pi垂线上距离Pj点为δ的P/点作平行于Pj切线的直线l,其方程为
(2Axl+B)x-y-A +C
+C δ
δ =0
=0
将Ax2+Bx+C-y=0代入,解得交点mi的x坐标分量为

式中 xt插补段起点的x坐标值;xmj插补段中计算点mj的x坐标值;Δxt插补段起点到终点沿x轴的步长。
插补段终点的x坐标值xt+1=xt+Δxt。将其代入抛物线方程得 yi+1=A +1+Bxi+1+C。于是,PjPt+1就是所要求的直线插补段。显然,这时的插补误差等于或小于σ,因此是可行的。
+1+Bxi+1+C。于是,PjPt+1就是所要求的直线插补段。显然,这时的插补误差等于或小于σ,因此是可行的。
所谓样条函数法,就是用样条软尺将指定的若干个点连成曲线,所得曲线不仅通过给出的点,而且是光滑的,并具有连续曲率。该曲线称为样条曲线,对样条曲线进行数学模拟得到的函数,即称为样条函数。样条函数的主要特点是,在联接点处具有一阶和二阶导数的连续性。若用一样条函数S(x)描述〔a,b〕区间的N+1个型值点,则S(x)应满足的条件为:1.其一阶和二阶导数在〔a,b〕区间内保持连续;2.在每一个区间〔xj-1,xj〕上S(x)都是一个三次多项式;3.应有S(xj)=yj(其中j=1,2,…N)。这样的样条函数S(x),称为三次样条函数。用样条软尺连接相邻的一些型值点,很象一根细的简支梁,受一定弯矩而产生弹性变形。细梁上的弯矩M(x)与各点挠度的曲率半径R(x)呈反比,即

而R(x)可用1/y″(x)代替,因此
M(x)∞y″(x)
可见,可用Mj表示S(xj)的二阶导数S″(xj),即
SN(xj)=Mj
由条件1已知二阶导数是连续的,并在〔xj-1,xj〕区间呈线性变化,故有

令hj=xj-xj-1,代入上式,经整理得

对上式积分二次,并进行整理得

该式就是S(x)在每个区间〔xj-1,xj〕的公式,为三次多项式。式中的未知数是Mj-1、Mj(j=1,x,…n),在整个S(x)上共有n+1个未知数,即M0、M1、…Mn。利用S(x)在样条型值点xj上具有一阶导数连续的条件,可求出未知数M0、M1、…Mn:

当x=xf时,可将上式化简为:

同理

若将S(x)在子区间〔xf-1,xf〕右端点xf的一阶导数值记作S(x-),在子区间〔xf,xf+1〕左端点xf的一阶导数值记作S′(xf+),则

由于型值点xf外的一阶导数是连续的,故有
S′(xf-)=S′(xf+)
代入值,并整理得

上式给出了n-1个联立方程(f=1,2,…n-1),若决定n+1个量(M0,M1,…Mn),还必须另外规定两个端点条件。常遇到的端点(边界)条件有:1.给出两端点xc和xn处的二阶导数,即M0= ,Mn=
,Mn=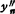 ,常取
,常取 =0,
=0, =0,称为自由端点条件,其几何意义是在x0的左边及xn的右边各与一直线相切;2.给出两端点x0和xn处的一阶导数S′(x0)=y0′,S′(xn)=yn′,这时可由式(8.5- 163)和式(8.5-164)得到:
=0,称为自由端点条件,其几何意义是在x0的左边及xn的右边各与一直线相切;2.给出两端点x0和xn处的一阶导数S′(x0)=y0′,S′(xn)=yn′,这时可由式(8.5- 163)和式(8.5-164)得到:

端点条件的一般形式

式中,当λ0=μn=0时为第1种端点条件;当λ0=μn=1时为第2种端点条件。
在一些情况下,端点条件往往未明确给出,这就需要采用一些方法予以确定。可选用的方法如:1.对于周期样条函数,有yn=y0,xn=xc,Mn=M0。若同时规定yn+1=y1,Mn+1=M1,hn+1=h1,则可得n+1个联立方程。2.可设M0=λM1,Mn=λMn-1(λ通常取1/2),或设M0=M1,Mn=Mn-1等作为端点条件。3.求出端点斜率。其方法有:
①过P0、P1、P2三点和Pn-2、Pn-1、Pn三点分别作圆,用P0点和Pn点的圆的切线斜率作为 和
和 的近似值。
的近似值。
②过P0、P1、P2三点及Pn-2、Pn-1、Pn三点分别作抛物线(y=Ax2+Bx+C),用过P0点和Pn点的抛物线的切线斜率作为y0′和yn′的近似值,即: =2A0x0+B0
=2A0x0+B0 =2Anxn+Bn
=2Anxn+Bn
③当给出n+1个列表点,又知列表曲线在端点附近与已知直线相切,但未给出切点值时,可采用抛物线法求端点与斜率。如图8.5-157所示,已知列表曲线与直线y=Kx+b相切,过点(x1,y1)和点(x2,y2)引抛物线与直线相切于(x0,y0)点,现设λ为待定系数,则该抛物线的方程为
y=Kx+b+λ(x-x0)2
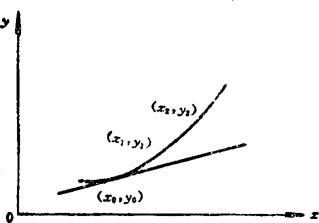
图8.5-157 抛物线与直线相切
由于抛物线过(x1,y1)点和(x2,y2)点,故下两式成立:
y1=Kx1+b+λ(x1-x0)2
y2=Kx2+b+λ(x2-x0)2
消去λ,得 ( )=
)=
因为x1>x0、x2>x0,所以上式开方取正值,

由此得 x0= ;y0=Kx0+b;
;y0=Kx0+b; =K
=K
(xntyn)点的计算方法与上相同。
④当端点与已知圆相切时,也可采用抛物线法求端点与斜率。如图8.5-158所示,过点(x1,y1)和点(x2,y2)引抛物线与已知圆(x-α)2+(yb)2=R2相切于(x0,y0)点,现设λ为待定系数,则可列抛物线方程


由上两式消去λ,得


图8.5-158 抛物线与圆相切
在抛物线与圆相切的切点处(x0,y0),两y0及两y0′相等,故有

用迭代法或二分法对上式求解,即可得到x0。
样条函数计算程序已标准化,可供选用。但在数控编程中,除给出列表点数值外,还需给出端点条件,方可调用标准程序求解。
对样条函数的直线或圆弧插补,有圆弧—圆弧相切法、直线公切两圆法和双圆弧相切法。
圆弧—圆弧相切的插补方法如图8.5-159所示。Pj(xj,yi)、Pi+1(xt+1,yt+1)为样条函数S(x)上的两个型值点。由S(x)可以得到y′(Pt),y′(Pi+1)以及y”(Pt),y″(Pj+1),于是可按式(8.5-151)和式(8.5-152)计算出该点曲率圆的圆心和半径:Ot(at,bj)、Rj和Oi+1(αi+1,bi+1)、Ri+1。图a)为两圆内含,b)为两圆相离,c)为两圆相交。由图可得:
l=PjOi+1=
m=OtOi+1=


故可求出圆心OT(a,b)的坐标:


图8.5-159 凸弧的三种情况

可求得切点PT(xT,yT)的坐标为:
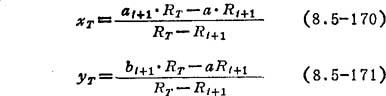

上述结论对于凹弧情况同样适用。对于两已知圆为一凸一凹的情况,如图8.5-160所示,由于在△OTPjOi+1中,OTOt+1边所对的角为180°-a,故求RT公式的符号不同,即
这种情况下的圆心坐标为:

切点PT(xT,yr)的坐标公式与凸弧情况相同,即可采用式(8.5-170)和式(8.5-171)求取。
这种圆弧插补的精度以样条函数S(x)为基准进行检查,以切点PT到S(x)的法线距离ε表示误差,如图8.5-161所示。因误差值很小,故可近似认为△PVPsPr为一直角三角形,于是
ε=(yV-yT)cosλ
式中的yV可由xT值代入S(x)中求得,而

若ε>Δ插,则在Pi+1、Pi间加密一点,即令


图8.5-160 一凸一凹的情况

图8.5-161 插补误差示意图
只要Δ插不是规定得太小,很少加密就可满足精度要求。
直线公切两圆的插补有多种情况。如图8.5-162所示,Pt(xt,yt)、Pt+1(xf+1,yi+1)为样条函数S(x)上的两个型值点,Rl、Ol(al,b1)为Pt点的曲率半径和圆心,Ri+1、Oi+1(at+1,bt+1)为Pi+1点的曲率半径和圆心。当(yl-bl)(yl+1-bl+1)>0时,为两圆弧同凸同凹情况。两圆弧同凸同凹情况下的公切线AB的斜率tgW的求法是:当Rl+1>Rl时,OtC与x轴夹角为W、OlOi+1与x轴夹角为U、∠COlOl+1=V;Rl>Ri+1时,Oi+1C与x轴夹角为W、∠COi+1Ot=V。W、U、V角度范围均在-π/2与π/2之间。W、U角取顺时针为正,逆时针为负。

图8.5-162 直线公切两凸圆弧
V角随Rt与Rt+1的大小取正或取负。于是



两圆弧同凹时,W=U-V,则

可由以下两方程式解出切点的坐标值

凸圆弧时: =
= (8.5-176)
(8.5-176)
y =
= }
}
凹圆弧时:
 } (8.5-177)
} (8.5-177)
切点坐标为:

同理可求出B切点的坐标:

凸圆弧时:

凹圆弧时:

当(yt-bt)(yi+1-bi+1)<0时,为两圆弧一凸一凹情况。在这种情况下,要有公切线两圆必须相离,如图8.5-163所示。由图可得:

图8.5-163 直线与一凸一凹圆弧相切

当Pt点在凸弧上,Pt+1在凹弧上时(yt>bt,yt+1<bt+1),W=U+V,则

切点坐标:

当Pt点在凹弧上,Pt+1点在凸弧上时(yt<bi,yl+1>bt+1),W=U-V,则

切点坐标:


插补精度的校验,如图8.5-164所示,

图8.5-164 直线公切两圆弧的误差
取Pt、Pt+1两点在x轴上间距的中点Pm作为检查点,CD为插补误差。则

将xD代入样条函数S(x)中求出yPm,则
PmD=yPm-yD
CD=PmDcosW (8.5-186)
若CD>Δ插,则表明插补误差超差,可在Pi, Pi+1中间加密一点(一般选Pm点),再按二圆公切线法进行计算,直至精度满足要求。
图8.5-165所示为双圆弧相切法。已知Pt(xt,yt)和Pi+1(xi+1,yi+1)为样条函数S(x)的两型值点。其Q点坐标:
yQ= (xQ-xt)+yl
(xQ-xt)+yl

式中 和
和 +1由S(x)求得。求解上两式得
+1由S(x)求得。求解上两式得


图8.5-165 双圆弧相切法示意图
求EPI和DPi+1。ΔQPiPi+1的三个边分别为


式中,、h分别为△QPtPt+1内切圆半径和△QPiPi+1的高。h/γ=b/DRi+1。于是得

由图可得EPi=EP,DPi+1=DP,求xP,yP:

求圆心Ot、Ot+1坐标:


求解上两式得

同理,通过求解Pt+1Oi+1和POi+1方程得


插补误差检验时,取P点作为检查点,将xP代入S(x)求出yV则应有
(yV-yP)cosa≤Δ插 (8.5-191)
否则需在Pt、Pt+1点间增加加密点,重复上述计算,直到满足精度要求。应该说明,双圆弧相切法只适用于同凸、同凹的列表曲线,即y″的符号不应改变。
6.5.5 立体型面零件的数值计算
以直线为母线的曲面或曲面回转体,如图8.5-166所示椭圆锥体,即其母线是与z轴夹角为θ的直线,xoy底面上的回转轨迹为椭圆的简单立体型面,这类零件可在立式加工中心或三坐标数控铣床用球头刀或圆弧盘铣刀采用“行切法”加工。加工过程中,刀具沿xoy平面运动一圈,在零件轮廓上加工出平面曲线,然后在z方向移动一个行距Δz,再加工出新的平面曲线,直至整个零件表面加工完毕。就加工每一平面曲线来说,其数值计算方法与平面零件的数值计算方法相同。对于立体型面,还需解决以下两点:

图8.5-166 椭圆锥体加工
①行距ΔZ的确定。采用球头铣刀加工时,每两行之间留下的刀痕构成了加工表面的微观不平度,行距越大微观不平度高度h越大。两行间球头铣刀中心线距离S≈ ,从而可得
,从而可得

式中的Φ=90°-θ,为母线与xoy平面的夹角。
②球头铣刀半径R刀在加工截面上的投影r的计算。在加工截面内计算刀具中心轨迹时,应该用γ作为刀具半径:
r=R刀sinΦ (8.5-193)
只要数控系统具有三坐标,两坐标联动控制功能就可完成简单立体型面的加工。三坐标运动,两坐标联动的数控加工编程方法通常称为 坐标编程。
坐标编程。
对于三坐标立体型面,如图8.5-167所示,其中Φ角是指每行加工截面上某一接触点的切面与xoy面的夹角,r=R刀sinΦ。各点的Φ角是变化的,因此γ也是变化的。
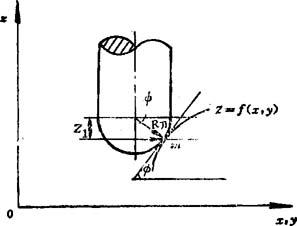
图8.5-167 三坐标立体型面加工示意图
在xoy平面,m点处零件轮廓的切线与x轴的夹角为θ,在xoz平面、m点处零件轮廓的切线与x轴的夹角为α。
则

γ= (8.5-195)
(8.5-195)
若零件轮廓以z=f(x,y)给出,则

变换为y=(x,z)后,

如图8.5-168所示,对于各行的xoy截面中的刀具中心轨迹,可通过以下计算求得:

图8.5-168 xoy截面中的刀具中心轨迹
x′N-1=xm-1-γm-1sinβm-1
y′N-1=ym-1-γm-1cosβm-1
xN=xm-γmsinβm-1
yN=ym-γmcosβm-1
过(x -1,y
-1,y -1)和(xN,yN)两点作直线
-1)和(xN,yN)两点作直线
y=K1x+b1

相邻两直线的交点:

在节点处,球头刀球心相对加工截面的高度(参见图8.5-167)为:Z1=R刀cosΦ。工件相邻两加工截面间距离(行距)ΔZ,如图8.5-169所示。

图8.5-169 行距ΔZ和刀具中心变化量
球头刀中心的变化量:
OiO2=Δx+R刀(cosΦ2-cosΦ1) (8.5-200)
如图8.5-170所示,球头刀由截面Ⅰ到截面Ⅱ在x和y方向的位移为:
Δx=xm1-xm2-r1sinθ1+γ2sinθ2 (8.5-201)
Δy=ym2-ym1-r1cosθ1+r2cosθ2 (8.5-202)

图8.5-170 x和y方向的位移