行星轮转速的计算

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册中》第1994页（1111字）

对于图5．7-1所示轮系，行星轮轴线平行于轮系主轴线，可用转化机构法求得行星轮转速nc。即：

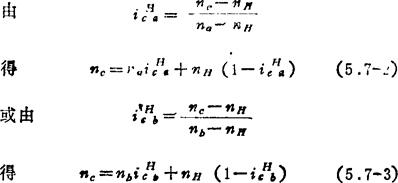
如图5．7-5所示由圆锥齿轮组成的行星轮系，因其行星轮轴线与中心轮和系杆的轴线不平行，故行星轮的转速不可用转化机构法计算，而应用矢量图法求解。

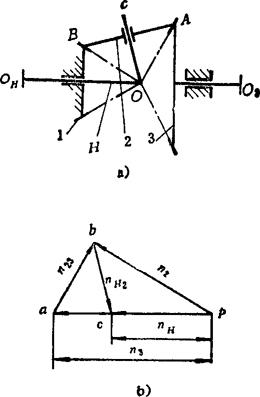
图5．7-5 转速矢量法求行星轮转速

根据运动学原理，构件的转速可以表示为沿其旋转轴线的一个矢量，称为转速矢量。其表示法规定如下：

① 矢量的方位沿构件的转动轴线。对于作复合转动的构件，绝对转速矢量沿绝对转动的轴线，相对转速矢量沿相对转动的轴线，牵连转速矢量沿牵连转动的轴线。

② 矢量的方向按右手法则决定。

③ 矢量的大小等于转速的绝对值。

例5．7-1 如图5．7-5所示圆锥齿轮行星轮系，若已知各构件尺寸，轮1固定不动，轮3主动，转速为n3，试求行星轮2的转速n₂及系杆的转速n₄。

解：先选定长度比例尺，绘制机构简图(见图5．7-5a)，再写出作复合转动的行星轮的转速矢量方程

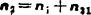
式中 n₂为轮2的绝对转速矢量；n₁为轮1的绝对转速矢量，也是轮2的牵连转速矢量；n₂₁为轮2相对轮1的相对转速矢量，其方位沿相对转动的瞬时轴线即啮合节圆锥的母线OB。因为n₁=0，所以n₂=n₂₁。这说明n₂与n₂₁大小相等，方向一致。

同理，行星轮2的转速矢量方程为：

该矢量方程只有两个未知量，可应用矢量多边形求解。在选定转速比例尺μn后，作矢量多边形(见图5．7-5b) 可解得行星轮2转速

n₂=μ_n·pb

把矢量pb平移到图a)的OB轴线上，按右手法则，可确定行星轮2的转向。

系杆H转速矢量方程式如下：

作矢量多边形(见图5．7-5b)可解得系杆H转速

nH=μ_n·pc

将矢量pc平移到系杆H的转动轴线OO_H上，用右手法则可确定系杆的转向。由图看出，pc和pa指向相同，即轮3和轮2的转向相同。