锁止弧

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册中》第2053页（1076字）

锁止弧半径的确定，如图5．11-2所示，对△O₁O₂H应用余弦定理，并将各边长表达为齿轮参数可得

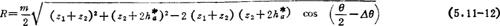
式中△θ为厚齿单侧齿顶弧厚△_s所对中心角，一般取△s≈0．5m，所以

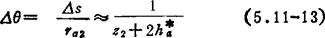
如图5．11-2和5．11-4所示，首齿即将入啮时，凸锁止弧末点应在两轮连心线上，否则将提前或滞后开锁而发生干涉，因此首齿啮入角φ_E或φ_K就是以首齿对称线为准的凸弧末点位置角，同样，末齿即将出啮时，凸弧始点也应在连心线上，否则将发生闭锁提前或滞后，所以末齿啮出角φF就是以末齿对称线为准的凸弧始点位置角。φ_F、φ_E、φ_K值的计算分别如下：

①φ_F的计算：对图5．11-2中的△O₁O₂F应用正弦定理，并以齿轮参数表达各边长，经整理可得啮点位置角计算式

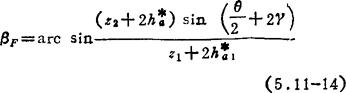
再依渐开线齿廓几何关系可得锁止弧始点位置角计算式

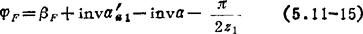
此式也适用于图5．11-4所示渐开线始啮情况下的啮出角计算。

② φ_E的计算：分析图5．11-2中△O₁O₂E的三角学关系，可得尖点始啮情况下的入啮点位置角计算式

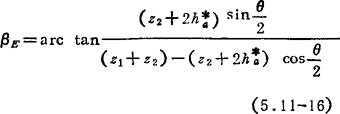
再依渐开线齿廓几何关系可得锁止弧末点位置角计算式：

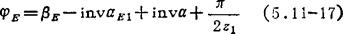
式中a_E1为首齿入啮点压力角，可按下式计算：

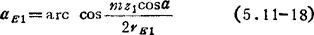
其中r_E1为主动轮入啮点半径。对△O₁O₂E应用余弦定理可得

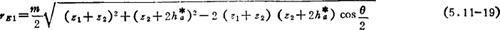
③φ_K的计算：渐开线始啮时，首齿对称线与两轮连心线之问恰含K／2齿距角(2π／z₁)，且渐开线始啮仅出现于K=2，所以锁止弧末点位置角为：

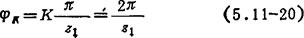
K=2、3、4、5时z₁、z₂值不同搭配下的φ_E与φ_F角的值参见表5．11-1、5．11-2、5．11-3、5．11-4。在表5．11-1中，若φ_E的值空缺，则表明该种齿数搭配属于渐开线始啮，须按式(5．11-20)计算φK值。