几何计算示例

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册中》第2056页（3005字）

渐开线齿外啮合不完全齿轮机构的几何计算式汇总于表5．11-5。

表5．11-5 渐开线齿外啮合不完全齿轮机构几何计算

例5．11-1 如图5．11-1a)所示机构，求其动停比。已知：z₁=40、z₂=15、z=14、K=2、N₂=1、N₁=2(具有实线及虚线所示的两个齿段)，a=20°。。

解1：按计算式求解。

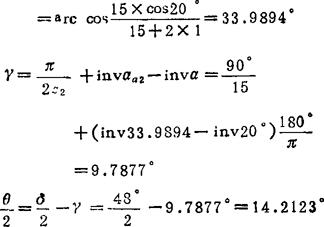
因 a₀₂一a=33．9894°-20°=13．9894°

可见，，即该机构为尖点始啮。

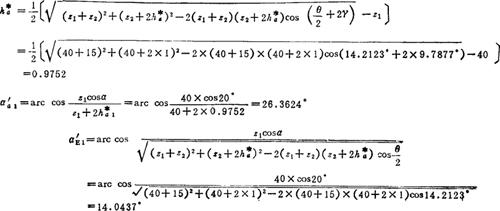
经以上计算可知，该机构的动停比为3．28。

解2：用查表法求解。

查表5．11-1可知，K=2、z₁=40、z₂=15时，=9．00°、φ_F=11．95°。于是

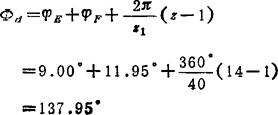
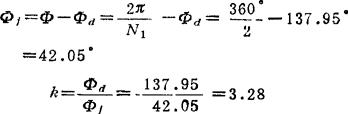
可见查表法甚为简便。

例5．11-2 要求主动轮每转一周从动轮动停一次(即N1=1)，从动轮每转一周停歇五次(即N2=5)，动停比k=1／3，允差±5%。试进行设计计算以确定不完全齿轮机构的结构参数z₁、z₂、_z、K、h₁、R、φ_E(或φ_K)和φ_F。

本例的求解步骤如下：

① 由于z₂必须是N₂的整倍数，可取z₂=…30、35…等，故现试取z₂=45。

② 由图5．11-5可知，当z₂=45时，K可取为2或3。现试取K=3。

③ 计算z值(按表5．11-5序9)：

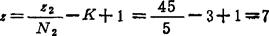
④ 计算Φ值：

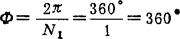
⑤ 求应有的Φ_d

应有 Φ_d=τΦ=0．25×360°=90°

⑥ 估算z₁值：

取φ_E+φ_F≈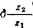⁽¹⁾，则由式5．11-3可得

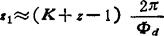
代入K=3，z=7，Φ_d=90°，得

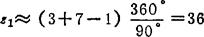
⑦ 查表5．11-2可知，当K=3、z₁=36、z₂=45时，h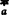=0．826、φ_E=14．78°、φ_F=17．53°。

⑧ 计算实际动停比：

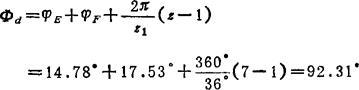
可见，与题意要求的k=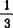相比较其误差为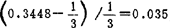，在±5%允差之内．

至此，虽已可以确定z₁、z₂、z、K、h₁、φ_E、φ_F，然后计算R，即可结束设计计算，但为比较不同方案，也可再求取另一组参数。现重复上述步骤，先取z2=30、K=2，再计算得z=5。Φ=360°，应有的Φ_d仍为90°，估算得z₁=24，查表5．11-1得h₁=0．544，φ_F=18．81°。因表中φ_E值空缺，可知为渐开线始啮，故计算

k=0．3524．此k值误差为0．057，已超出允差．为寻求第三方案，仍取z₂=30、K=2，但改取z₁=25，再重复步骤⑦、⑧，得h₁=0．511，φ_F=18．04°．φ_k=14．4°，Φ_d=90．04°．k=0．334．显然，这一方案动停比误差仅为0．0006，优于第一方案，应予采用。

确定了z₁、z₂、K后，计算R值：

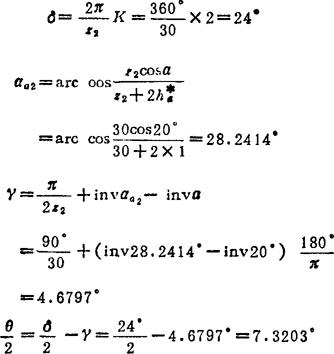
取△s=0．5m，则

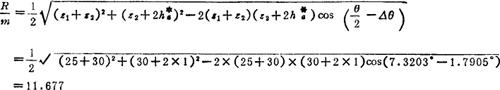
当从强度或其它条件确定m后，R也就确定了。

例5．11-3 绘制图5．11-1a)、b)两机构的i₂₁和φ₂随φ₁而变化的线图(示意)。图a)机构数据见例5．11-1；图b)机构数据见例5．11-2。

解：图a)机构在定传动比时i₂₁=z₁／z₂=40／15≈2．67；由例5．11-1的解可知Φ_d=137．95°，且为尖点始啮，故可示意绘出i₂₁～φ₁曲线如图5．11-6中的线1。当φ₁由零增至Φ_d时，φ₂由零增至ψ===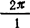2π，以后轮2则保持不动，由此可绘出线2。同理，可绘出表示虚线齿段i₂₁、φ₂的线3、线4。

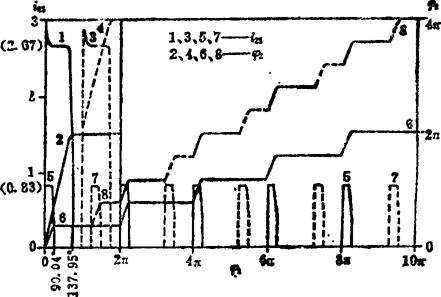
图5．11-6 i₂₁和φ₂随φ₁而变化的线图(例5．11-3)

图b)机构在定传动比时i₂₁=z₁／z₂=25／30≈0．83；由例5．11-2的解可知Φd=90．04°，且为渐开线始啮，故可绘出线5。当φ₁由零增至Φ_d时，φ₂由零增至ψ=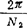=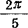，当φ₁继续增至2π之前，轮2保持不动，由此可绘出线6。轮1转一周后，运动重复进行，φ₂逐次递增，当轮1转5周角时，轮2转1周角，由此可绘出线6-6。虚线7是虚线齿段的i₂₁；线6-8-8是具有不均布的虚线齿段时的φ₂。

例5．11-4 不完全齿轮副几何尺寸设计图示例。图5．11-7中主动轮首齿齿顶圆半径的公差按IT11级标准公差确定，末齿按IT9级。首齿齿顶圆半径的上偏差取为某一负值(－0．07)，以确保不发生齿顶干涉(因首次重合度足够大，为1．587，故公差还可增大，比如可按IT12)。末齿齿顶圆半径下偏差取为某一正值(+0．05)，以便能将从动轮推到应有的停歇位置。凸锁止弧半径、凹锁止弧半径及其位置尺寸(49．69)的公差按IT6或IT7级，且均取负偏差。锁止弧表面粗糙度可取或凸锁止弧始末点位置角取负偏差，半径较大时角度公差宜取小，反之可取大。这里的角度公差(6＇)，相当于允许始末点沿圆周方向可有0．2mm的位置变动。

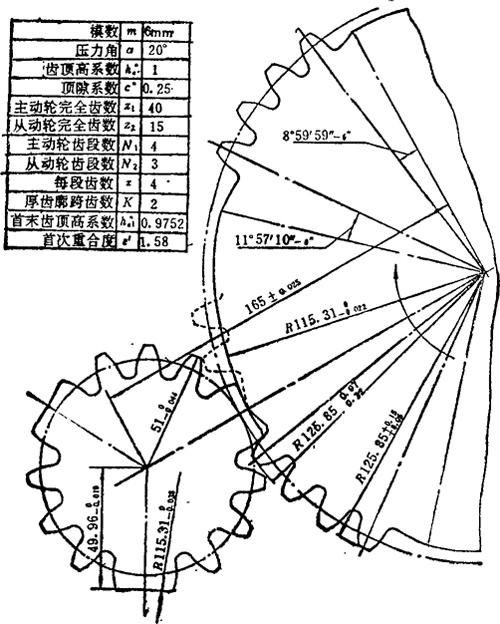
图5．11-7 几何尺寸图 (例5．11-4)