数学模型的表达式

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册上》第726页（676字）

由于最优化设计中的设计变量可以看作组成设计空间的坐标分量，设计空间中每一个点就是一个设计点，该设计点的一组坐标分量即代表一个设计方案的设计变量值。因此，在最优化设计中的设计点，可以看作和这组设计变量对应的、以坐标原点为始点的一个矢量X的端点。该矢量可以用矩阵表示，即

于是，最优化设计的数学模型也可以表示为：

求设计变量 X=［x₁，x₂…x_n］^T

极小化目标函数 F(X)

满足约束条件 g_l(X)≥0，j=1，2，…，mh_l(X)=0，j=(m+1)，(m+2)，…p

另外，最优化设计的数学模型还可以用集合的概念来表达，即

minF(X)

X∈Rⁿ

s．t．g_l(X)≥0，j=1，2…，mh_l(X)=0，j=(m+1)，(m+2)…，p

式中 X∈Rⁿ表示设计变量属于n维实数空间；“s．t．”(有的文献上写成“sub．”)是英文“subject to”的缩写，在这里表示“满足于”的意思。上式也可以写成：

mioF(X)

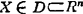
D=｛X|g_l(X)≥0，j=1，2，…，m；h_l(X)=0，j=(m+1)，(m+2)，…p｝

式中表示设计点X必须在约束条件组成的可行域(记作集合D)中，而该可行域又包含于全体n维矢量集合构成的n维实数空间Rn中。