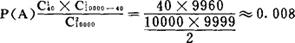古典概率

出处：按学科分类—经济 湖北人民出版社《企业管理公式辞典》第28页（554字）

指在概率论发展初期的某些情况下，利用所研究的事件本身所具有的物理或几何的“对称性”，直接计算概率的一种方法。假设基本事件的全体是有限的，每个基本事件的发生是等可能的(即它们发生的概率相等)，且两两互相排斥。如果基本事件的总个数为n，事件A由其中m个基本事件组成，那么，事件A出现的概率可由下列公式计算：

并把它称作古典概率。古典概率具有如下基本性质：(1)事件A的概率P(A)在区间〔0，1〕上取值，即：0≤P(A)≤1；(2)必然事件的概率为1，不可能事件的概率为0，即：P(U)=1，P(V)=0。

例如，设在10000个零件中有40个零件是次品，从中任取2个，问：其中只有一个是次品的概率为多少?

解：从10000个零件中任取2个，所有可能取法的个数就是基本事件总数n，即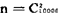个；设事件A：“2个中只有一个次品”(即一次取2个，一个是次品，另一个必定是合格品)的取法有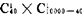：，此即事件A中所含的基本事件数m，故有：