线性规划数学模型

出处：按学科分类—经济 湖北人民出版社《企业管理公式辞典》第335页（1220字）

线性规划是《运筹学》中的一个主要分支，在经济管理中已得到了广泛的应用。在企业的生产经营活动中，可以用来解决下面一些问题：有限资源的合理利用；制定最优的生产计划；原材料的合理下料；物资运输最优调配；机床负荷的安排；作业排序；厂址选择及工厂布局；生产任务的分配与工作安排等等。

用线性规划解决企业管理中的问题的步骤大致如下：

(1)把企业生产经营活动中的具体问题，抽象成一组数学方程，建立数学模型。

(2)对统计数据和资料(包括经济和技术的)进行处理，为线性规划模型提供必需的和可靠的原始数据。

(3)采用一定的方法求出问题的最优解，作为生产经营管理的依据。

(4)监督和控制最优方案的实施。

(5)对最优方案进行灵敏性分析，考虑到原问题中的一切条件(指各种由统计资料得到的参数)，受外界干扰而发生变化，当这种变化超出一定范围而影响方案的最优解时，及时采取措施调整方案。

具有下述形式的模型称为线性规划数学模型：

模型中：X_j表示结构变量(或决策变量)；C_j表示目标函数系数；b₁表示资源数(或右边常数)；a_ij表示技术系数，表示单位j产品对第i种资源的消耗量。

通常，把极大化目标，所有约束均为“≤”的模型称为线性规划模型的一般形式(或典型形式)。

典型形式的和式表达式：

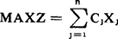
典型形式的矩阵表达式：

例：某厂生产甲、乙两种产品，主要消耗煤、电力、人工三种资源。甲产品每吨产值7万元，乙产品每吨产值12万元。生产每种产品一吨，对以上三种资源的需用数量如下表所示。

现有煤360吨，电力200千瓦小时，人工300人日。问该厂如何安排生产，使产值最大?

设生产甲产品X1吨，乙产品X₂吨，则可建立使产值最大的线性规划数学模型：