分段函数
书籍:高中数理化公式定理大全
出处:按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第14页(684字)
在函数y=f(x)中,对于自变量x的不同取值,有着不同的对应法则,这样的函数通常称为分段函数,如函数
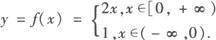
就是分段函数,分段函数是一个函数,而不是几个函数.
例 已知函数y=f(x)定义域是[0,1],求g(x)=f(x+a)+f(x—a)的定义域.
分析 这是复合函数求定义域,由x+a,x—a来决定,又含有字母,注意对字母参数的一切允许值分类讨论.
解析 由y=f(x)的定义域是[0,1],所以函数g(x)的定义域为下列不等式组的解集:
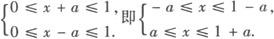
也就是区间[—a,1—a]与[a,1+a]的交集,比较两区间左、右端点,可知:
当—1/2≤a<0时,
g(x)的定义域为{x|—a≤x≤1+a};
当0≤a≤1/2时,
g(x)的定义域为{x|a≤x≤1—a}.
当a>1/2或a<—1/2时,上述两区间的交集为空集,这时g(x)不能构成函数.
上一篇:求函数定义域的主要依据
下一篇:高中数理化公式定理大全目录