等比数列的性质
书籍:高中数理化公式定理大全
出处:按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第27页(909字)
(1)若m+n=p+q,则am·an=ap·aq.
(2)每隔k项(k∈N+)取出一项,按原来顺序排列,所得的新数列仍为等比数列.
(3)数列{an}为等比数列,则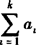 ,
, 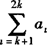 ,…,
,…,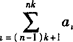 ,也成等比数列.
,也成等比数列.
例1 在等比数列{an}中,已知a3+a6=36,a4+a7=18,an=1/2,求n.
解 设等比数列{an}的公比为q.
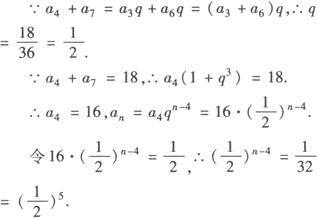
则n—4=5,即n=9.
评注 本题灵活地应用an=amqn—m,使问题解得简单、明了、快捷.
例2 有四个数,其中前三个数成等差数列,后三个数成等比数列且第一个数与第四个数的和是16,第二个数与第三个数的和是12,求此四数.
分析 本题求四个数,设四个未知数,再去求解是可行的,为了减少消元的麻烦,也可以利用条件来减少未知数的个数.
解 前三个数依次为a—d,a,a+d,则第四个数为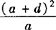 依题意
依题意
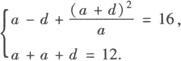
解此方程组,得a1=4,d1=4或a2=9,d2=—6
故所求四数为0,4,8,16,或15,9,3,1.
例3 等比数列{an}中,a1+an=66,a2an—1=128,前n项的和Sn=126,求n和公比q.
分析 利用等比数列的性质,建立a1、an的方程组求出n与q.
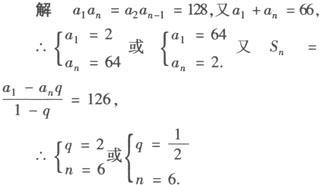
上一篇:等比数列的判定方法
下一篇:数列求和有以下几种方法