推广
书籍:高中数理化公式定理大全
出处:按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第56页(1152字)
如果a1,a2,…,an∈R+,且n>1,则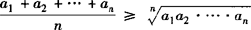 ((当且仅当a1=a2=…=an时取“=”号).
((当且仅当a1=a2=…=an时取“=”号).
例1 已知圆锥的底面半径为R,高为3R,在它的所有内接圆柱中,全面积的最大值是( ).
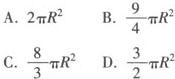
分析 本题考查了圆锥与圆柱的基本计算,同时考查了利用均值不等式求最值.
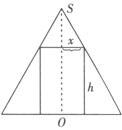
解 如图作圆锥的轴截面图,设内接圆柱的底面半径为x,高为h,则由三角形相似可得:
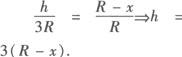
∴圆柱的全面积为:
S全=2πxh+2πx2
=2πx·3(R—x)+2πx2
=2πx(3R—2x)
=π·2x(3R—2x)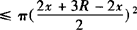
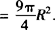 .
.
当且仅当2x=3R—2x即x=3/4R时取“=”号,故选B.
评析 本题也可用二次函数求最值
例2 a>b>1, ,Q=1/2(1ga+lgb),
,Q=1/2(1ga+lgb),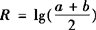 ,则( ).
,则( ).
A.R C.Q 分析 本题考查了对数的基本性质及均值不等式的应用. 故R>Q,从而选B. 评析 本题也可用特殊值法来判定,如果a=100,b=10,很容易选B,解这类题要善于利用特例法求解,利用均值不等式和函数单调性比较大小是常用的方法. 例3 设x、y、z为正数,x2+y2+z2=1,试求 解 若a、b、c∈R+,则由平均值不等式可知:a2+b2+c2≥ab+bc+ca∴(a+b+c)2≥3(ab+bc+ca), 当且仅当x=y=z时取得最小值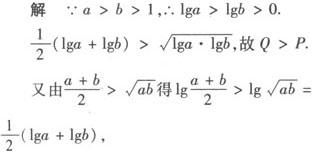
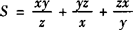 的最小值.
的最小值.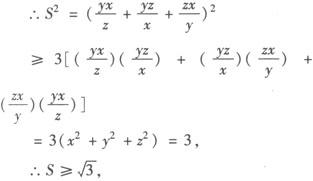
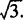 .
上一篇:均值不等式
下一篇:高中数理化公式定理大全目录
.
上一篇:均值不等式
下一篇:高中数理化公式定理大全目录