由方程画它的曲线

出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第68页（1718字）

由已知方程画出它的曲线，基本方法是描点法，但在描点以前必须对方程f(x，y)=0进行如下讨论：

(1)范围：就是讨论方程中x，y取值范围，一般f(x，y)=0解出y=f(x)，求x的取值范围，由f(x，y)=0解出x=φ(y)，求y的取值范围．

(2)对称性：在方程f(x，y)=0里，若以—x代x而方程不变，则它的曲线关于y轴对称，若以—y代y而方程不变，则它的曲线关于x轴对称，若以—x代x同时以—y代y而方程不变，则它的曲线关于原点对称．

(3)截距：在方程中令y=0，求x的实数解，即为曲线在x轴上的截距(横截距)，在方程中令x=0，求y的实数解，即为曲线在y轴上的截距(纵截距)．

弦长公式：(直线与曲线相交时)

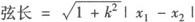
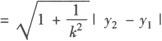
(k为直线斜率)．

求曲线的方法：

1．代入法 2．直接法

3．几何法 4．定义法

5．参数法

例1 已知直线l∶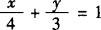，M为直线l上的一个动点，过点M作x轴和y轴的垂线，垂足分别为A、B，求把有向线段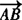分成的比λ=2的动点P的轨迹方程．(代入法)

解 设M(x₀，y₀)，P(x，y)，则A(x₀，0)，B(0，y₀)，

∵P分有向线段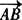所成的比λ=2，

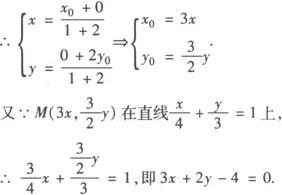
点评 代入法体现了数形相互转化的思想．

例2 已知线段AB的长为3，平面上一动点M到A的距离是到B的距离的两倍，求动点M的轨迹方程．(直接法)

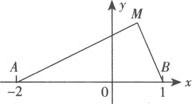
解 如上图所示，在线段AB上取一点O，使|AO|=2|OB|，以O为原点，AB为所在直线为x轴建立直角坐标系，则A、B两点的坐标分别为(—2，0)，(1，0)．

设动点M的坐标为(x，y)，则点M属于集合P={M||MA|=2|MB|}，

于是有

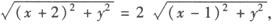
平方化简得：x²+y²—4x=0，即为所求的轨迹方程．

点评 用直接法求轨迹方程时，往往需要选择恰当的坐标系，否则容易造成计算繁琐且方程形式复杂．

例3 作方程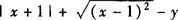=0所表示的曲线．(几何法)

分析 训练学生的变形能力，培养学生的分类讨论思想．

解 原方程变形为|x+1|+|x—1|—y=0．

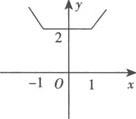
当x≥1时，方程为y=2x；

当—1

当x≤—1时，方程为y=—2x．

点评 本题的难点是将方程进行变形去掉两个绝对值符号，从而培养学生的分类讨论的思想．