圆的一般方程
书籍:高中数理化公式定理大全
出处:按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第69页(618字)
由圆的标准方程展开,得x2+y2—2ax—2by+a2+b2—r2=0,其外形为x2+y2+Dx+Ey+F=0,称为圆的一般方程,配方得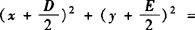
 ,其方程式的特点:
,其方程式的特点:
①x2,y2项系数相等且不为0;
②没有x·y这样的交叉项.
二元二次方程Ax2+Bxy+Cy2+Dx+Ey+F=0表示圆的充要条件:
若上述的二元二次方程表示圆,则有:A=C≠0,B=0这只是二元二次方程表示圆的必要条件,但不充分.
当A=C≠0,B=0时,上述二次方程可化为: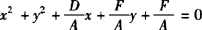 ,此方程表示圆的条件是
,此方程表示圆的条件是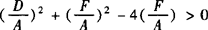 即D2+E2—4AF>0.
即D2+E2—4AF>0.
故有二元二次方程Ax2+Bxy+Cy2+Dx+Ey+F=0表示圆的充要条件是:
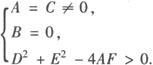
把圆的一般方程x2+y2+Dx+Ey+F=0(D2+E2—4F>0)化为标准方程的一般步骤:
可先把方程左边分别按x,y配方,之后把常数移到右边,即得: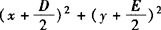
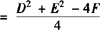 ,进而可得到圆心坐标
,进而可得到圆心坐标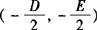 ,半径
,半径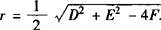 .
.
上一篇:圆的标准方程
下一篇:高中数理化公式定理大全目录