等角定理的推论
书籍:高中数理化公式定理大全
出处:按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第88页(1105字)
如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等.
例1 如图,E,F分别是长方体A1B1C1D1—ABCD的棱A1A,C1C的中点,求证:四边形B1EDF是平行四边形.
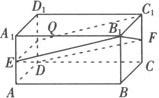
策略 平行四边形是平面图形,若能证得四边形的一组对边平行且相等,那么这个四边形就是平行四边形.
证明 设Q是DD1的中点,连结EQ,QC1.
∵E是AA1的中点,
∴ .
.
又在矩形A1B1C1D1中 ,
,
∴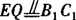 (平行公理),
(平行公理),
∴四边形EQC1B1为平行四边形,
∴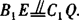 .
.
又∵Q、F是矩形DD1C1C的两边中点,
∴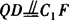 ,
,
∴四边形DQC1F为平行四边形,
∴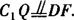 .
.
又∵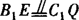 ,∴
,∴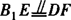 ,
,
∴四边形B1EDF为平行四边形.
点评 三线平行公理是我们证明分别在两个平面的两条直线平行的常用工具.
例2 如下图所示,在正方体AC1中,M、M1分别是AD、A1D1的中点.
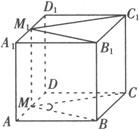
求证:∠BMC=∠B1M1C1.
策略 证明角相等,利用空间等角定理是常用的思考方法,另外也可以通过证明两个三角形全等或相似来证明两角相等.
解法一 连M1M,M1、M分别是A1D1和AD的中点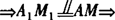 四边形AMM1A1为平行四边形
四边形AMM1A1为平行四边形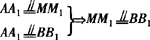
 四边形BB1M1M为平行四边形
四边形BB1M1M为平行四边形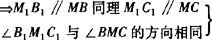
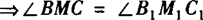
解法二 同上可让四边形M1B1BM为平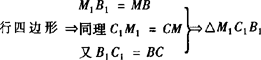 ≌△MCB
≌△MCB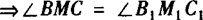
上一篇:异面直线的判定定理
下一篇:高中数理化公式定理大全目录