函数极限的运算法则
书籍:高中数理化公式定理大全
出处:按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第123页(1222字)
如果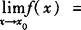 a,
a,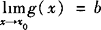 ,那么
,那么
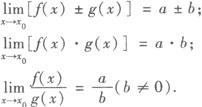
【说明】 在进行函数极限的运算时,还经常用到下面的结论:
(1)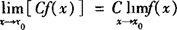 (C是常数);
(C是常数);
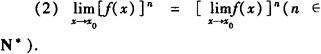
一个重要结论:
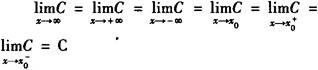
例1 讨论下列函数当x→+∞,x→—∞和x→∞时的极限.
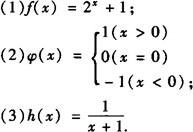
解 根据函数f(x)当x→+∞,x→—∞,x→∞时极限的定义,观察函数值变化的趋势,结合函数图象得出的结论.
(1)由下图可知,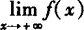 不存在,
不存在,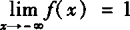 ,
,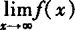 不存在.
不存在.
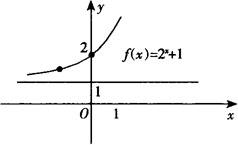
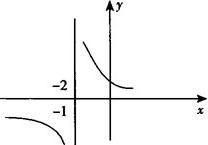
(2)由下图可知,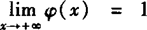 ,
,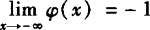 ,
,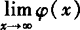 不存在.
不存在.
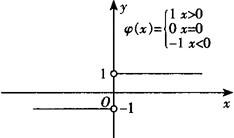
(3)由图可知,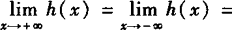 0,∴
0,∴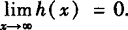 .
.
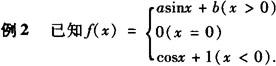
当a,b取何值时,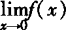 存在,其值为多少?
存在,其值为多少?
解 x=0是此分段函数的分界点,而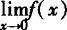 存在的充要条件
存在的充要条件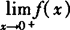 与
与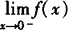 都存在并且相等∴
都存在并且相等∴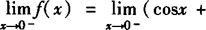
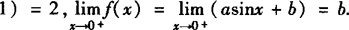 .
.
∴当b=2,a取任意常数时,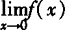 存在,其值为2.
存在,其值为2.
例3 研究函数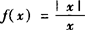 在x=0处的左、右极限.
在x=0处的左、右极限.
解 由于x<0时,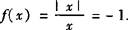 .
.
所以当x→0—时,f(x)→—1,
故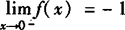
而当x>0时,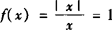 ,
,
∴当x→0+时,f(x)→1,
因此,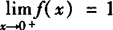 .
.
由于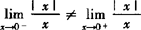
所以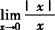 不存在.
不存在.
探索延拓创新
例4 求证: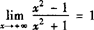 .
.
解 对照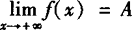 的定义进行证明.
的定义进行证明.
注意到当x>0时,有

上一篇:函数极限存在的一个充要条件
下一篇:数列极限的四则运算