平方根的性质

出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《初中数理化公式定理大全》第20页（1573字）

1．一个正数有两个平方根．

2．0只有一个平方根，它是0本身．

3．负数没有平方根．

注意 1．平方根包含算术平方根，算术平方根是平方根中的一个．

2．只有非负数才有平方根和算术平方根

3．0的平方根和算术平方根都是0．

4．一个正数有两个平方根，而一个正数的算术平方根只有一个．

5．正数a的平方根表示为±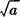，正数a的算术平方根表示为．

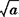6．正数的算术平方根，一定是正数，而正数的平方根则一正一负，且它们互为相反数．

7．负数没有平方根，也没有算术平方根．

例1 计算“16/25的平方根”正确的是( )．

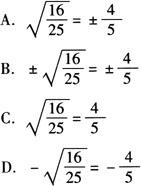
答 B．

[解析] 正数的平方根有两个，表示为±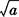的形式．

例2 如果一个正数的平方根为2a－7和a+4，求这个正数．

解 由题意得，(2a－7)+(a+4)=0．

所以a=1，此时2a－7=－5，a+4=5．

而(－5)²=5²=25，所以这个正数是25．

[解析] 由平方根的意义，“一个正数的平方根有两个，它们互为相反数”，故可依此求出a的值，进而求出原来的正数．

例3 下列说法正确的是( )．

A．36的平方根是6

B．16的算术平方根是±4

C．

D．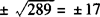

答 D．

[解析] A错在正数36的平方根有两个它们是±6；

B错在正数16的算术平方根有一个是+4；

C错在负数没有平方根和算术平方根．

例4 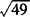的平方根是＿＿，算术平方根是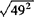＿＿，的平方根是＿＿，算术平方根是＿＿．

答 ±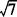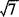，，±7，7．

[解析] 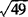本身等于7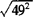，本身等于49．

注意分清到底是求哪个数的平方根或算术平方根．

例5 当x＿＿时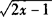，有意义．

答 ≥1/2．

[解析] 正数和0都有算术平方根，

故2x－1≥0即x≥1/2时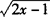，有意义．