公式法

出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《初中数理化公式定理大全》第43页（1602字）

用求根公式解一元二次方程的方法称为公式法．

注意 1．一般地，对于一元二次方程ax²+ bx+c=0(a≠0)，当b²－4ac≥0时，它的根x=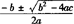，这个式子称为一元二次方程的求根公式．

2．公式法的意义在于，对于任意的一元二次方程，只要将方程化为一般形式，就可以直接代入公式求解．

3．公式法解一元二次方程的步骤：

(1)把方程化为一般形式．

(2)确定a，b，c的值．

(3)若b²－4ac≥0，代入公式求解．

若b²－4ac<0，说明方程无实数解．

4．当b²－4ac>0时，方程有两个不同的根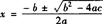

当b²－4ac=0时，方程有两个相同的根

当b²－4ac<0时，方程无实数解．

例1 用公式法解方程：．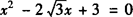

解 ∵a=1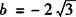，，c=3，

∴．

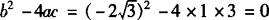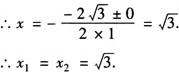
[解析] 当b²－4ac=0时，一元二次方程有两个相等的实数根，不能误认为只有一个根．

例2 用公式法解方程：

x²－x－1=0．

解 ∵a=1，b=－1，c=－1，

∴b²－4ac

=(－1)²－4×1×(－1)=5．

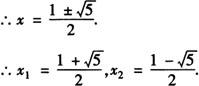
[解析] 当b²－4ac>0时，一元二次方程有两个不相等的实数根

例3 用公式法解方程：

3x²+7x+5=0．

解 ∵a=3，b=7，c=5，

∴b²－4ac=7²－4×3×5

=49－60=－11<0．

∴方程无实数根．

[解析] 当b²－4ac<0时，一元二次方程无实根．

例4 关于x的一元二次方程x²+(2k+1)x+k－1=0根的情况是( )．

A．有两个不相等实数根

B．有两个相等实数根

C．没有实数根

D．根的情况无法判定

答 A．

[解析] ∵b²－4ac=(2k+1)²－4(k1)=4k²+5>0，从而这个方程有两个不相等的实数根，选A．