一次函数的图象

出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《初中数理化公式定理大全》第57页（1899字）

一次函数y=kx+b(k≠0)的图象是一条直线．

注意 1．作一次函数图象时，只要确定两个点，再过这两个点作直线，就可以了．

2．一次函数y=kx+b(k≠0)的图象也称为直线y=kx+b(k≠0)．

3．一次函数表达式与图象间的对应关系：

(1)满足表达式的点在函数图象上．

(2)函数图象上点的坐标满足表达式．

4．正比例函数图象是一条过原点的直线．

例1 函数y=3x+1的图象一定通过( )．

A．(3，5) B．(－2，3)

C．(2，7) D．(4，10)

答 C．

[解析] 图象过点，也就是点在函数图象上，那么点的坐标就适合函数解析式，代进去，当x=2时，y=3×2+1=7．

故选C．

例2 已知点A(2，3)在直线y=2x+b上，则b等于( )．

A．－1 B．0

C．1 D．2

答 A．

[解析] 点在直线上，那么点的坐标适合直线方程y=2x+b．

即 3=2×2+b，∴b=－1．

故选A．

例3 若直线y=3x+6与坐标轴围成的三角形的面积为S，则S等于( )．

A．6 B．12

C．3 D．24

答 A．

[解析] 解这类题先求出直线与两坐标轴的交点，当x=0时，y=6；当y=0时x=－2，即直线与两坐标轴交点分别为(－2，0)、(0，6)画出草图，问题可迎刃而解．

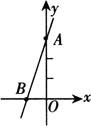
S_△AOB=1/2×|－2|×|6|=6．

例4 画出函数y=5x+15的图象，并利用图象求解下列问题：

(1)求方程5x+15=0的解；

(2)如果y的取值范围为－5≤y≤5，求x的取值范围；

(3)如果x的取值范围为－2≤x≤1，y的最大值和最小值是什么?

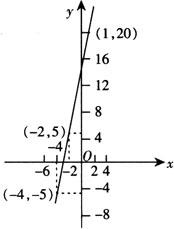
解

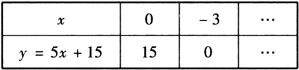
(1)当y=0时，图象与x轴交于－3，这－3就是5x+15=0的解，实际上也就是图象与x轴交点的横坐标．

(2)图象上看，如果－5≤y≤5，则－4≤x≤－2．

(3)从图象上看，如果－2≤x≤1，则5≤y≤20，x在此范围之内，y的最大值是20，y的最小值是5．

[解析] 用图象法可以帮助我们解决一些变化问题，是一种特殊实用的数学方法，解题时图象要画准确．

5x+15=0，5x+15<0，说明当函数y的值是某特定范围的值时，就得到了关于自变量x的方程或不等式，即对于y=5x+15，当y=0时，有5x+15=0；当y<0时，有5x+15<0．