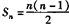线段的基本性质

出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《初中数理化公式定理大全》第81页（1807字）

两点之间的所有连线中，线段最短(两点之间，线段最短)．

注意 连接两点的线，包括曲线、直线、折线，其中最短的一条是连接两点的线段，如图所示．

例1 校园大道两旁种植树木，定下两棵树的位置就能定下一排树的位置，这是因为＿＿．

答 经过两点有且只有一条直线．

例2 把一条弯曲的公路改成直道，可以缩短路程，其道理用几何知识解释为( )．

A．线段可以比较大小

B．过两点确定一条直线

C．两点之间线段最短

D．线段有两个端点

答 C．

例3 C是线段AB外一点，那么AB＿＿BC+AC，AC＿＿BC+ABBC＿＿AB+AC简述理由＿＿．

答 <，<，<，两点之间线段最短

例4 过平面上任意四点中的两点画直线，可以画出不同直线的总的条数为( )．

A．4条

B．6条

C．4条或6条

D．1条或4条或6条

答 D．

[解析]

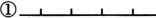
四点在

同一条直线上．

②

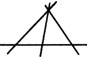
三点在同一条直线上

③

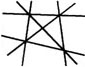
任意三点不在同一条直线上．

例5 如图，有A、B、C、D四个村庄，为解决当地缺水问题，政府准备投资修建一个蓄水池，不考虑其他因素，请你画图确定蓄水池P点的位置，使它与四个村庄的距离之和最小．

答 如图所示．

[解析] 根据两点之间线段最短．

例6 阅读以下材料并计算．

平面上有n个点(n≥2)，且任意三个点不在同一直线上，过这些点作直线，一共能作多少条不同的直线?

解 (1)分析：当仅有两点时，可连成1条直线．

当有三个点时，可连成3条直线．

当有四个点时，可连成6条直线．

当有五个点时，可连成10条直线．

(2)归纳：考察点的个数n和可连成直线的条数S_n．

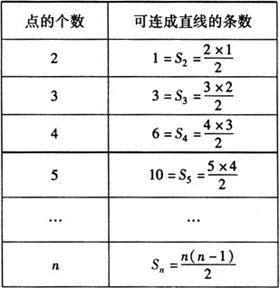
(3)推理：平面上有n个点，两点确定一条直线，取第一个点A有n种取法，取第二个点B有(n－1)种取法，所以一共可连成n(n－1)条直线，但AB与BA是同一条直线，故应除以2，所以．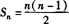

(4)结论：