线段垂直平分线的性质

出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《初中数理化公式定理大全》第110页（2976字）

线段垂直平分线上的点到这条线段两个端点的距离相等．

注意 用几何语言描述如下：

如图：因为l是AB的中垂线，且P点在l上．

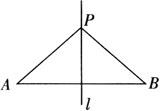
所以PA=PB．

例1 如图，在等边△ABC中，∠B和∠C的平分线相交于O，BO、OC的垂直平分线分别交BC于E和F，请说明：BE=EF=FC．

证明：连接OE、OF．

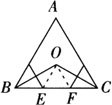
∵E、F分别是BO、OC的垂直平分线上的点，

∴OE=EB，OF=FC．

又∵△ABC是等边三角形，且OB、OC分别平分∠B、∠C，

故∠OBE=∠BOE=30°，

∠OCF=∠COF=30°，

可得∠BEO、∠CFO均为120°，

∴∠OEF=∠OFE=60°．

∴△OEF是等边三角形，

∴BE=OE=OF=EF=FC．

∴BE=EF=FC．

[解析] 用线段垂直平分线可以证明线段相等．

例2 如图，AD是△ABC中∠BAC的平分线，AE=AC，EF∥BC，请说明：∠FEC=∠DEC．

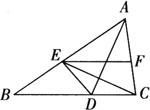
证明：∵AE=AC，AD是∠A的平分线．

∴AD是EC的垂直平分线．

∵D是EC的垂直平分线上的点，

∴DE=DC，∴∠DCE=∠DEC．

∵EF∥BC，

∴∠FEC=∠ECD，

∴∠FEC=∠DEC．

[解析] 用线段垂直平分线的性质可以证明角相等．

例3 如图，AD⊥BC于D，∠B=2∠C，请证明：AB+BD=DC．

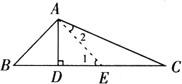
证明：在DC上截取DE=BD，连结AE．

∵AD⊥BC，DE=BD，

∴AD是BE的垂直平分线．

∵点A在AD上，

∴AB=AE，∠1=∠B．

∵∠1是△AEC的外角，

∴∠1=∠2+∠C．

又∵∠B=2∠C，

∴∠2+∠C=2∠C．

∴∠2=∠C．

∴AE=CE．

∵CE+DE=DC，

∴AB+BD=DC．

[解析] 用线段垂直平分线性质可以证明线段之间的和、差关系．

例4 如图，△ABC中，AB=AC，DE垂直平分AB，AB+BC=10cm，则△DBC的周长=＿＿cm．

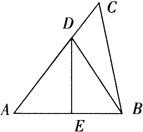
解 ∵DE垂直平分AB，

∴AD=DB．

△DBC的周长=DB+DC+BC

=AD+DC+BC

=AC+BC

=AB+BC

=10(cm)．

[解析] 用线段垂直平分线可以求线段长．

例5 如图，AC⊥BD，DF是AB的垂直平分线，EC=EF，求∠A的度数．

解 连结BE．

∵AC⊥BD，DF⊥AB，且EC=EF，

∴BE是∠ABC的平分线．

∴∠1=∠2．

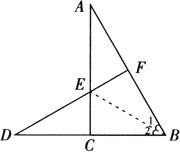
又∵DF是AB的垂直平分线，

∴EA=EB．∴∠1=∠A．

在Rt△ABC中，∠A+∠ABC=90°．

即∠A+∠1+∠2=90°．

∴3∠A=90°，

∴∠A=30°．

[解析] 用线段垂直平分线可以求角度

例6 公路MN的一边有A、B两个工厂，他们准备在公路MN的旁边合建一座仓库P，要求到两厂的距离相等．请你在图上把点P找出来．

解法

[解析] ①作AB的中垂线与MN交于P点．

②用线段垂直平分线性质可以解决实际问题．