相似三角形的性质

出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《初中数理化公式定理大全》第136页（1521字）

1．相似三角形的对应角相等，对应边成比例．

2．相似三角形对应高的比、对应角平分线的比和对应中线的比都等于相似比．

3．相似三角形周长的比等于相似比．

4．相似三角形面积的比等于相似比的平方．

例1 两个相似三角形的对应高的比为5∶7，其中一个三角形的周长比另一个三角形的周长小4cm，求这两个三角形的周长．

解 相似三角形对应高的比等于相似比，对应周长的比等于相似比．设较小三角形的周长为xcm，则较大三角形的周长为(x+4)cm．

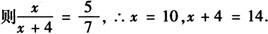
所以两个三角形的周长分别为10cm、14cm．

例2 已知：如图，在△ABC中，D为AB边上一点，E为AC边上一点，△ADE∽△ABC，若AD=3，AB=6，DE=2．5．

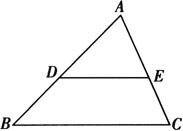
(1)求BC的长；

(2)证明DE∥BC．

答 (1)因为△ADE∽△ABC，所以=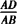

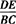
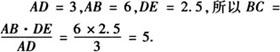
(2)因为△ADE∽△ABC，所以∠ADE=∠ABC．

所以DE∥BC．

例3 三个相似三角形面积和为232cm²，对应边之比是2∶3∶4，则这三个三角形面积分别是＿＿．

答 32cm²，72cm²，128cm²．

[解析] 根据相似三角形面积之比等于相似比的平方．

设三个三角形面积分别为x₁cm²，x₂cm²，x₃cm²则x₁∶x₂∶x₃=4∶9∶16．

∵三个三角形面积和为232，∴每份．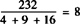

∴三个三角形面积分别为4×8=32，9×8=72，16×8=128．

例4 如图，有一块三角形土地，它的底边BC=100m，高AH=80m．

某单位要沿着底边BC修一座底面是矩形DEFG的大楼，D、G分别在边AB，AC上，若大楼的宽DE是40米，求这个矩形面积．

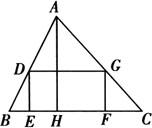
解 由已知条件可知△ADG∽△ABC．

根据相似三角形对应高的比等于对应边的比．

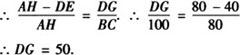
∴矩形面积S=50×40=2000(m²)．

[解析] 解决三角形内接矩形或内接正方形这类问题，常用办法是根据相似三角形对应高的比等于相似比的性质．