直角三角形相似的应用

出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《初中数理化公式定理大全》第137页（1160字）

测量

例1 为测量电视塔AB的高度，小亮在他与电视塔之间竖立一根5米高的标杆(即CE)，当他距标杆2米时(即点D处)，塔尖A、标杆的顶端E与眼睛F恰好在一条直线上，已知小亮的眼睛距地面的高度是1．6米，标杆距电视塔的距离是108米，求电视塔的高度，

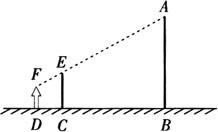
解 如图过F点作FG∥DC交CE于H，交AB于G．

则△AFG∽△EFH．

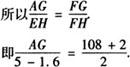
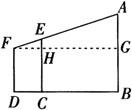
解得AG=187．

所以AB=188．6米

[解析] 利用直角三角形相似解决问题

例2 如图(1)河对岸A处有一村庄，河这边C处有另一村庄．怎样计算两个村庄的距离?请设计出计算方案．

图(1)

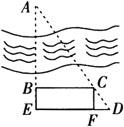
图(2)

下面是小亮设计的一种方案，并根据实地测量得到的数据，给出了解答过程：

他从C点沿正西方向走到B点，使B点恰好位于A点的正南方向上，然后向南走到E点，并量得BE=40m，再从E点向东走到D点，使得点D，C，A恰在一条直线上．量得ED=100m，DC=48m，如图(2)可计算AC的长．

解 作CF⊥ED垂足是F，因为BE=40m，ED=100m，CD=48m．

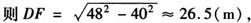
BC=ED－DF≈73．5(m)．

设AC=xm，则AD=(x+48)m．

因为BC∥ED，所以∠ABC=∠AED

∠ACB=∠ADE．

所以△ABC∽△AED．

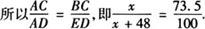
解得x≈133．

答：两村庄的距离约为133m．