关于线段垂直平分线的3个定理

出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《初中数理化公式定理大全》第146页（832字）

1．线段垂直平分线上的点到这条线段两个端点距离相等．

2．到一条线段两个端点距离相等的点在这条线段的垂直平分线上．

3．三角形三条边的垂直平分线相交于一点，并且这一点到三个顶点的距离相等．

注意 前2个定理是一对互逆定理．

例1 如图所示，已知AB=AC，AD平分∠BAC，E是AD上一点，求证：EB=EC．

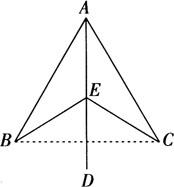
证明 连接BC．

∵AB=AC，AD平分∠BAC，

∴AD⊥BC，且AD平分BC．(等腰三角形三线合一)

又∵E是AD上一点，

∴EB=EC．(线段垂直平分线上的点到这条线段两个端点距离相等)

例2 如图所示，在△ABC中，AB的中垂线DE交AC于E，垂足为D．

若AC=6cm，BC=4cm．

求：△BCE的周长．

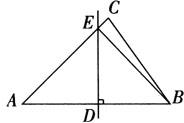
解 ∵ED为AB的中垂线，

∴AE=BE． ∵AC=6cm，BC=4cm，

∴△BCE的周长=BC+BE+EC=BC+AE+EC=BC+AC=6+4=10(cm)．