直线和圆的位置关系
出处:按学科分类—文体、科学、教育 商务印书馆国际有限公司《初中数理化公式定理大全》第168页(2087字)
直线和圆有三种位置关系:
1.直线和圆相交,即圆心到直线的距离d 2.直线和圆相切,即圆心到直线的距离d=r(半径). 3.直线和圆相离,即圆心到直线的距离d>r(半径). 注意 直线和圆的位置关系与圆心到 直线的距离d与半径r之间的数量关系可以相互转化. 例1 已知☉O的直径为13cm,直线l与圆心O的距离为d. (1)当d=5cm,直线l与圆的位置关系是__. (2)当d=13cm时,直线l与圆的位置关系是__. (3)当d=6.5cm时,直线l与圆的位置关系是__. 答 相交、相离、相切. [解析] 根据d与r的数量关系判定直线l与☉O的位置关系. 例2 ☉O的直径是10,直线l与☉O相交,则圆心O到直线距离d满足__. 答 0≤d<5. [解析] 相交的特殊情况是直线过圆心时圆心O到直线l的距离d=0. 例3 ☉O的半径r=5cm,点P在直线l上,若OP=5cm,则直线l与☉O的位置关系是( ). A.相离 B.相切 C.相交 D.相切或相交 答 D. [解析] 当直线与圆相交,交点恰为P的话,则OP=5(半径)这种情况容易忽略. 例4 Rt△ABC中,∠C=90°,AC=3,BC=4,以AB的中点O为圆心,r为半径作圆,则此圆与直线AC、BC都相离的条件是( ). A.r>2.5 B.r<2 C.r<1.5 D.r<1 答 C. [解析] 如图所示,过O分别作OM⊥AC于M点,ON⊥BC于N点,则OM、ON分别为△ABC的中位线,所以OM=1/2BC=2ON=1/2AC=1.5. 要使所作圆与直线AC、BC都相离,则r<1.5且r<2,也就是r<1.5即可. 例5 已知△ABC中,∠C=90°, (1)要使☉C与直线AB相切,求☉C半径. (2)若☉C的半径为2,则☉C与直线AB的位置关系怎样? (3)若☉C的半径为 解 (1)过C作CD⊥AB于D点. 在Rt△ABC中 ∵∠C=90°,BC=2, 根据勾股定理可得AB=4. ∴AB·CD=AC·BC. (点C到直线AB的距离) 要使☉C与直线AB相切,则半径r=CD= (2)当☉C半径r=2时, ∵2> ∴☉C与直线AB相交. (3)当☉C半径 ∵ ∴☉C与直线AB相离.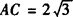 ,BC=2,以C为圆心画圆☉C.
,BC=2,以C为圆心画圆☉C.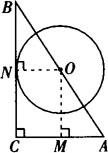
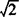 ,则☉C与直线AB的位置关系怎样?
,则☉C与直线AB的位置关系怎样?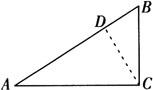
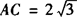 .
.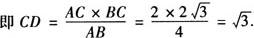
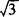 .
.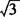 ,
,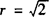 时.
时.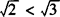 ,
,