圆心距

出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《初中数理化公式定理大全》第171页（1154字）

两圆圆心之间的距离．

两圆相切与“圆心距d、两圆半径R、r之间的数量关系”的等价关系．

d=R+r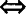两圆外切．

d=R－r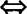两圆内切．

注意 这也是两圆位置关系与“d与R，r之间数量关系”的相互转化．

例1 已知两圆外切时，圆心距为12cm，两圆内切时，圆心距为3cm，求两圆半径．

解 设两圆半径分别为Rcm、rcm，依题意可得

答 两圆半径分别为7．5cm、4．5cm．

例2 若两圆的半径分别为R、r(R>r)，圆心距为d，且有R²+d²－r²=2Rd，判断两圆的位置关系．

解 ∵R²+d²－r²=2Rd，

∴R²－2Rd+d²=r²．

∴(R－d)²=r²．

∴R－d=r或R－d=－r．

即d=R+r或d=R－r．

∴两圆外切或内切．

例3 如图，已知A点坐标为(0，3)，☉A的半径为1，点B在x轴上，若☉B过点M(2，0)且与☉A相切，求B点坐标．

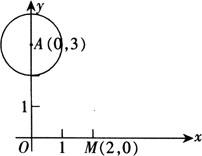
解 设B点坐标为(x，0)显然x<2根据题意，☉B半径r_B=2－x．

两圆圆心距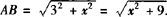

当两圆外切时AB=r_A+r_B．

即．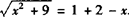

∴x²+9=(3－x)²，解得x=0，此时B点坐标(0，0)．

当两圆内切时，AB=r_B－r₄．

即．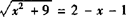

∴x²+9=(1－x)²，解得x=－4，此时B点坐标(－4，0)．