有限差分法

出处：按学科分类—自然科学总论 山东人民出版社《方法大辞典》第183页（1405字）

主要是用于求偏微分方程的数值解。

解题步骤大致如下：

(1)在定解区域G上进行网格剖分，即用平行于坐标轴的直线将G分成许多小区域，这些线的交点称为网格结点，数值解就是求微分方程的解在结点上的近似值。

(2)用差商代替微商，将微分方程用差分方程代替。

(3)解差分方程。

例1．考虑拉普拉斯方程第一边值问题：

这里P是单位正方形的边界。

采用正方形网格，结点(x_i，y_j)，简记为(i，j)，

X_i=ih， y_j=jh

称为步长，用u_ij表u(x_i，y_j)的近似值，记，

利用，，代入(1)。即得差分方程组：

u_i，j－1+ui－_1，j+u_i+1，j+u_i，j+1－4u_i，j=0 (2)

i，j=1，2，…，n－1。

其中边界点u_0，j，u_u，j，u_i，0，u_i，n可由相应的φ值给出，组(2)的未知量是｛u_i，j｝，i，j=1，2，…，n－1，它可由一般迭化法或超松弛迭代法求解之。

例2．考虑二维热传导方程：

取定时间步长为τ，x与y方向的步长为，记u在结点(x_i，y_j，t_k)=(ih，jh，kτ)的近似值为u，(i，j=0，1，…，n，kτ≤T)，

由(3)知：，，其余的可逐层解出，即若已知u在t=t_k层的值，则在t=t_k+1层上的值可由下列差分格式求出：

这里，需解方程组求出。

此格式分为两步，首先按(4)，固定j=j₀(j₀=1，2…，n－1)，求出过渡层上的，然后按(5)，固定i=i₀(i₀=1，2，…，n－1)，求出t=t_k+1层上的；在每一步上，只需求解三对角系数矩阵的方程组。

例3．考虑波动方程：

取时间步长为τ，x方向的步长为，记为u在结点(x_i，t_k)=(ih，kτ)处的近似值。

由已知条件知：，，；将用差商代替可得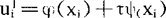，假设已求出了u在t=t_k－1及t=t_k层的值，，则t=t_k+1层上的值，通常可由下列Von－Neumann 格式求出：

记λ=τ／h，当1／4≤α≤1时，λ可任意取值，当时，λ必须满足不等式。特别取α=0时称为显格式。

取时，称为隐格式。