多项式插值法

出处：按学科分类—自然科学总论 山东人民出版社《方法大辞典》第193页（856字）

已知函数f(x)在n+1个不同点X_n，x₁，…x_n上的函数值为f(x_i)=y_i，i=0，1，…n。

要求一个次数不超过n的多项式P_n(x)，使满足：

P_n(x_i)=f(x_i)，i=0，1，…n。 (1)

这就是n次代数插值问题。

条件(1)称为插值条件，x₀，x₁…x_n称为插值节点。P_n(x)称为f(x)的n次插值多项式。

满足(1)的插值多项式可表为：

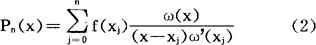
其中ω(x)=(x－x₀)(x－x₁)…(x－x_n)，ω’(x_j)表ω(x)在X_i点的导数。(2)通常称为拉格朗日形插值多项式。

(2)也可用下述牛顿形插值多项式给出：

P_n(x)=f(x₀)+f(x₀，X₁)(x－x₀)+f(x₀，x₁，x₂)(x－x₀)(x－x₁)+…+f(x₀，X₁，…x_n)(x－x₀)(x－x₁)…(x－x_n－1) (3)

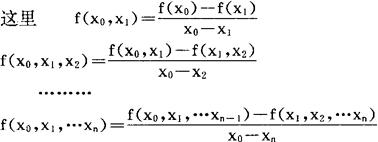
f(x₀，x₁，…x_k)称为f(x)在点x₀，x₁，…x_k上的k阶差商。

(3)中的节点常取作等距的，且按节点离开插值点x的远近来排列先后次序。

若f(x)在xi点的导数值f’(x_i)=y’i也为已知，则存在唯一的2n+1次多项式H(x)，它满足条件：

H(x_i)=y_i，H’(x_i)=y’i i=0，1，…n (4)

H(x)称为f(x)的厄米特插值多项式，可表为：