均值估计

出处：按学科分类—自然科学总论 山东人民出版社《方法大辞典》第203页（724字）

数论的重要方法。

在数论中经常要研究一个数论函数f(n)当n→∞时的性状。例如，能否找到一个简单的函数g(n)(如幂函数、对数函数等)使得当n→∞时，有f(n)～g(n)。但是数论函数值的分布往往是很不规则的。

例如，除数函数d(n)，当n=p时，它等于2；但当n=2^k时，它又等于kH，其中k=logn／log2。又如，若ω(n)表示n的不同素因子的个数，Ω(n)表示n的全部素因子的个数，即若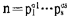时，ω(n)=s，Ω(n)=α1+…+α_s。显然，当n为素数时，ω(n)=Ω(n)=1；但当n通过2之乘方而趋于无穷时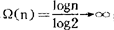，；而当n通过素数之连乘积，n=p₁p₂…p_s，而趋于无穷时，ω(n)=s→∞，因此，d(n)，ω(n)，Ω(n)之值是很不规律的，不能得到它们的渐近公式。

但是，它们的算术平均值，即下述的均值估计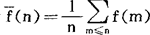，比起f(n)来往往要规则得多。例如，取f(n)=d(n)，容易证明它有以下的均值估计

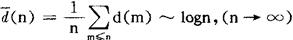
这时称d(n)的平均阶为logn。

对于函数ω(n)，Ω(n)则有以下重要的估计。

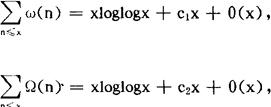
其中c₁，c₂为常数，由此便知ω(n)，Ω(n)的均值估计为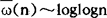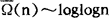， (n→∞)。

即它们的平均阶都是1og1ogn。

研究各种均值估计在数论中有极其重要意义。

在解析数论中，某些结果的改进往往要首先依靠某种均值估计的进一步改进。例如，关于哥德巴赫猜想的着名结果(1+2)，其关键就在于运用，一种新的加权筛法并证明了新的一类均值定理。