数学归纳法

出处：按学科分类—自然科学总论 山东人民出版社《方法大辞典》第281页（1051字）

根据归纳原理而应用演绎推理的一种特殊的数学证明方法。

数学归纳法的逻辑根据是自然数公理：“如果一个集合N含有1，而且含有自然数K的同时也含有它的后继的自然数K+1，那么N是全体自然数的集合”。

数学归纳法是证明同自然数集有关的(即含有自然数n的)命题或公式的基本方法，在许多数学学科中都要用到它。应用数学归纳法证明命题时必须包括两个步骤：

(1)证明当n=1时，所证命题是真实的；

(2)假定当n=k(k是自然数)时所证命题真实，然后从这个假定推导出当n=k+1时，所证命题也真实。

最后，根据归纳原理可以断言：当n取任何自然数时，命题真实，这样，就使命题的真实性获得无限的延拓。

因为。根据第一步，当n=1时命题真实，把这个结论当作第二步的假设(k=1)，从而有n=2时命题真实。

再把这结论作为下一步的假设(k=2)，从而有n=3时命题真实……，每个自然数总有一个而且只有一个比它多1的后继数，所以这样的论证，可以反复进行，无限制地继续下去。最后得出“当n是任何自然数时命题真实”的一般结论。

必须注意，用数学归纳法来证明命题时，上述的两个步骤中每一个都不可省略。如果只有(1)证明n=1时命题真实而没有(2)的证明，则这种证明方法成为不完全归纳推理，所得结论就不一定真实，但是第一步证明是数学归纳法的出发点，也不可省略去。

如果没有第一步的验证，则第二步证明就没有根据，于是“n=k时命题真实”只是一种假设，它的真实性还不能确定，从而结论是否真实也就不能确定。例如，对于等式，若假定n=k时等式成立，也可以证明n=k+1时等式成立，但不能得出结论；这等式对于任何自然数成立，因为当n=1时它就不成立(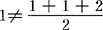)!实际上，对于任何自然数它都不成立!因此只有当上述两步都得到证明时，结论才能保证是真实的。

n也不一定从等于1开始，可以从某一自然数n0(n0＞1)开始。例如，在证明“n边多角形有n(n3)／2条对角线”的第一步中，应该令n0=3。这是由实际问题的性质决定的，因为事实上没有n<3的n边形。应该注意，这时的结论只能说：当n是大于或等于n0的一切自然数时，命题真实。