皮尔模型

出处：按学科分类—自然科学总论 山东人民出版社《方法大辞典》第425页（745字）

R·皮尔(R·Pearl)等人提出的一种模型。

其一般形式为：

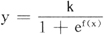
式中，k为常数，f(x)是自变量x的多项式，即

f(x)=a₀+a₁x+a₂x²+…+a_mx^m

最常用的f(x)为一次多项式，且其一次项系数为负值的情形，即

f(x)=a₀+a₁x，a₁＜0

写成增长曲线即为：

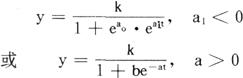
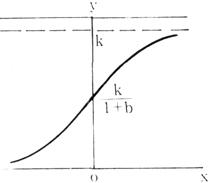
式中，b=e^a。，a=－a₁。下图绘出了这种常用的皮尔生长曲线。

从图中可以看出：

(1)当x→－∞时，y→0；

(2)当x=0时，y=；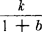

(3)当x→∞时，y→k。

即；当－∞＜x＜∞时，0＜y＜k，y=k是皮尔曲线的上渐近线，或称k是功能特性参数y增长的极限值。

若给出(x，y)的一组观测值数据，则只需求出式中的a，b，k三个参数即可求出拟合方程。

比较常用的方法有七种，即，费舍(Fisher)法、赫特林(Hotelling)法、尤拉(Yule)法、耐尔法(Nair)、若赫茨(Rhodes)法，选点法和倒数总和法。这些方法中，多为由给定数据估算出a，k值，然后推算b值。

另一些方法则是利用数据同时将a，b，k三个参数值求出。具体计算时，可根据所给数据的特征，选用不同的方法。