排队模型分类

出处：按学科分类—经济 中国财政经济出版社《中国物资管理辞典》第539页（763字）

根据排队系统三个基本组成部分的主要特征：(1)顾客相继到达的时间间隔分布，(2)服务时间分布，(3)服务台个数，将排队系统按照它们关于这三方面主要特征的不同组合，进行分类，形成为不同类型的排队模型。

为了简明地表示排队模型类型，现在广泛采用坎特尔(D．G．Kendall)的三要素标记法，以符号U／V／W表示：

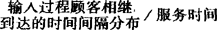
分布／服务台个数

用以表示顾客相继到达的时间间隔分布和服务时间分布的符号是：M即负指数分布，具有马尔科夫(Markov)性质；D即确定型的(Deterministic)定长输入或定长服务；E_K即K阶爱尔朗(Erlang)分布；GI即一般相互独立的随机分布；G即一般随机分布。根据上述的标记法，“M／M／1”表示到达间隔时间和服务时间为负指数分布和一个服务台的排队系统，“M／M／C”表示到达间隔时间和服务时间同上和C个并列服务台的排队系统，其他表示方式，可以依此类推。

一个排队系统，除了上述主要特征外，还有其它一些特征，如顾客源和排队容量是有限或是无限，服务规则是先到先服务还是随机服务等等不同条件。

为此，曾经提出将坎特尔的标记法增加三项，改为：

U／V／W／X／Y／Z

其中：U，V，W同坎特尔标记法，X表示系统中顾客限制数(以N表示系统最大容量，以∞表示容量无限制；Y表示顾客源的顾客数(以m表示顾客源是有限，以∞表示无限；Z表示服务规则(FCFS指先到先服务；LCFS指后到先服务；RSS指随机服务；PR指优先服务)。一般规定，如顾客源是无限的，队长没有限制；等待制服务规则是先到先服务；每个服务台是单个服务的排队系统，称为标准模型，可将X、Y、Z等标记省去。