指数平滑法
书籍:中国物资管理辞典
出处:按学科分类—经济 中国财政经济出版社《中国物资管理辞典》第568页(729字)
对时间序列的各项数据,以由选定的平滑常数α1并按等比级数逐项递减所形成的一系列的平滑系数,作为权数,进行加权平均来计算预测趋势值的方法。
其计算公式为:
St=αYt+α(1-α)Yt-1+α(1-α)2Yt-2++(1-α)tS0
以上公式经整理后可改写如下,以便利和简化计算:
St=αYt+(1-α)St-i1
=αSt-1+α(Yt-Sl-1)
式中:S0为估算的初始值;St和St-1分别代表时间t和t-1的指数平滑平均数。Yt代表第t时间的实际观测值。α代表平滑常数。指数平滑法同加权移动平均法一样,重视近期数据对预测值的作用,故给予较大的权数,但又并不完全不顾远期数据的作用,对时间序列的全部数据,按时间的远近,分别给予不同的权数。平滑常数α的取值范围为0<α<1,它对时间序列起修正的作用。α取较大的值,可以提高修正的作用,使计算的指数平滑平均数能迅速跟上实际观测值的变化。反之,α取较小的值,可使早期的数据特征,在指数平滑平均数中得到充分反映。一般可按均方误差最小的原则,作为评价α取值是否合适的尺度。指数平滑法取较大的α值,与移动平均法取较小的N值,具有同样的修匀效果,它们两者之间大致有如下的关系:
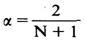
指数平滑法只要具备本期观测值和上期预测值两项数据,就可进行预测计算,需要储存的数据,大大减少,而且计算简便,费用较少,在短近期经济预测中效果较好,因此,是使用较为广泛的一种定量预测方法。
上一篇:二次移动平均法
下一篇:中国物资管理辞典目录