迪基－富勒(D－F)检验

出处：按学科分类—经济 经济科学出版社《西方经济学大辞典》第265页（1095字）

检验经济和金融变量是否是随机游走，这类研究利用了David Dickey和Wayne Fuller的单位根检验。

假定我们相信有增长趋势的变量Y_t可由下式描述

Y_t=α+βt+ρY_t－1+ε_t (1)

一个可能性是Y_t在不断的增长，因为它有正的趋势(β＞0)，但在剔除趋势后，它是平稳的(即|ρ|＜1)。在这种情况下，方程(1)的回归有意义。另一种可能性是Y_t在不断增长，因为它是个伴随正位移的随机游走(即α＞0，β=0且ρ=1)。这种情况，我们应该对△Y_t进行研究，将Y_t剔除趋势后也不是平稳的，方程(即使Y_t已剔除趋势)也将导致虚假的结果。

有人可能会想方程(1)可由OLS进行估计，关于ρ的t统计量可用于检验ρ是否显着不等于1。然而，如果ρ的真实值为1，则OLS估计是有偏的。

这样，以这种方式使用OLS将导致不该拒绝随机游走假设时而拒绝了。

方程(1)的一个问题是它隐含了一个假设，即误差项ε_t不存在序列相关。

我们经常在ε_t有序列相关时，也能进行单位根检验。这可由扩展Dickey-Fuller检验实现。

这个检验将方程(1)右边扩展为包含Y_t滞后变化量的项：

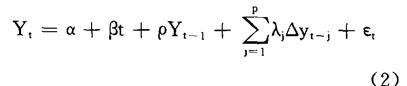
其中△Y_t=Y_t－Y_t－1。滞后项个数的选择标准是使误差项ε_t不存在序列相关。

此时的单位根检验步骤如下：首先，对无限制回归方程

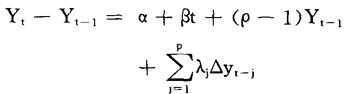
应用OLS进行估计。然后，对限制回归方程

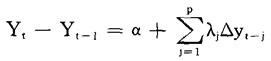
应用OLS进行估计。最后，计算出标准F比率用以检验限制(β=0且ρ=1)是否成立。我们必须使用Dickey和Fuller分布表来进行检验。

Dickey和Fuller分布表

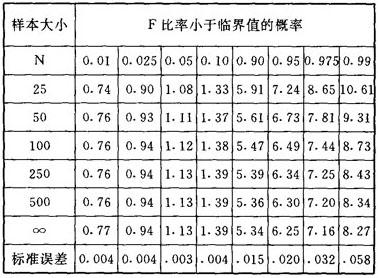
来源：Dickey and Fuller，op．cit．，Table VI，p．1063，1981．