贝尔不等式

出处：按学科分类—自然科学总论 天津人民出版社《自然辩证法辞典》第82页（542字）

指隐变数理论提出以后，1965年贝尔(Bell，J．)在“定域性”隐参量理论的基础上提出的一个不等式。

它指出冯·诺依曼关于量子力学完备性定理不能成立。当两个子系统相距很远时，它们之间有一定的定域性(或独立性)，这与量子力学的结构会有不同，设A(â，λ)是系统1的某个物理量观测值，â为仪器参数，λ为隐参量；B(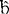，λ)为系统2的物理量观测值，â与B无关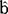，与A无关，设P(λ)为λ的某种统计分布，系统1和2相距甚远。

则A和B乘积的平均值为：

当变动仪器参数b为b′时，可以证明下述不等式成立

|P(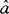，b)-P(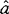，b′)|≤1+P(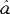′b′)贝尔首先证明了这个不等式，因此称贝尔不等式，按量子力学一般原理，系统1和2相距很远时，彼此还有关联，观测到的平均值不应该遵守上述不等式，问题是隐参量λ在其中起作用，这个标明定域性的隐参量λ是否存在有待实验上的证明。如果实验证明存在，那么隐参量理论就有了可靠的根据，作为量子力学的另一种解释成立。

因此贝尔不等式提出以后，对于持续达30年之久的量子力学解释上的争论，又是一个新的浪花，所以在60年代贝尔不等式的影响是很大的。