可近集与车贝雪夫集

出处：按学科分类—自然科学总论 北京出版社《现代科技综述大辞典上》第62页（4588字）

逼近论最早是1854年车贝雪夫考虑连续函数用n次多项式最佳一致逼近。

20世纪20～30年代经过F．Riesz、Kirchberger和Borel建立了存在性、唯一性、包含0特征性定理，及J．W．Young、V．Poussin和Haar等人的交错性特征定理，确立了Haar条件。此时，一方面平均佳逼有着名的Jackson唯一性定理，60年代起开始统一到考虑赋范空间(或度量空间)一点到某个集G的最近距离问题，开始了泛函逼近论，产生了可(逼)近集(即存在性集)、车贝雪夫集(即存在唯一性集)两种重要概念。

除紧集外，Riesz的有限维空间本征首先提供一类重要可逼近集。R．C．James到1972完全解决了自反空间的本征是它所定义连续线性泛函都有极大元，从而它的闭子空间都是可近集，此期间1960年R．R．Phelps的卓越工作首创了唯一性的对偶理论。

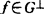X的闭子空间G具(U)性等价于X*中是车氏集，而G可近且具(U)性则推G是车氏集，但一般非等价。V．Indumathi 1987年沿对偶思想获得有极大元与G可近性的种种关系。

对超平面说，它可能是不可近的，其例子I．Singer、A．L．Garkavi都发现过，N．V．Efimov1961年引入近紧性及闭囿紧性，二者是介于紧性与可近性的。1964年Singer指出可近未必近紧，近紧未必囿紧。

近紧性深入研究见潘文熙1989和1991年的文章，一向难回答近紧集本征是什么，于1975年Koshev获知一致凸空间中，G近紧等价于G可近，度量投影P_G紧像且1，s，c。超平面ψ^－1(c)…的可近性等价于ψ有极大元。

但此命题推到有限余维m≥2情形是否成立?1982年F．Deutsch指出ψ₁，……ψ_m极大元存在仅是必要而非充分，1985年L．P．Vlasov找到有限余维G可近性的等价条件，乃U_x+G是闭的(U_x－单位球)，也等价于U_x／G闭。对闭凸集，则自反空间固然保证它可近性，但非自反空间仍是难题。

实例空间C(Q)，l¹，L^∞(Ω)等可近子空间研究以70年代Garkavi、Phelps与Singer1974年工作为代表，还有R．HolmesB．Kripke、J．Blatter。1983年R．Khalil与W．Deeb研究了L_p中可近集，对X中取值的空间C(Q，X)，L^p(μ，x)最基本问题是提升性即子空间Y和X中可近是否导致L_p(产，Y)在L_p(μ，x)中可近，K－D．二人已着手研究L^p(μ，Y)，对于C(Q，Y)A．Kamel于1986年找到了例子C(Q，Y)于C(Q，X)中不可近，且X有限维，Kamel的系列工作是与算子空间逼近问题联系进行的。

此外，1988年矫恒利研究了L_∞(μ，Y)。

可近性一个难研究问题是传递性，一般并不具备。

1971年W．Pollul首先用可近传递性表征自反性，1987年Indumathi引入Pollul空间P(n)，即X合乎于M可近，M于X可近，且dimX／G≤n则G于X可近，表明一定良好传递性。例如Co，遗憾的是无限维C(Q)与L¹(μ)都不是P(2)空间。

这方面工作可说是James工作的深化。

人们关注另一问题是给两个可近集F，G，何时才使F+G是可近集?Repess－Cheney1982年用了G中一个弱紧性条件推F+G可近。

M．Feder1987年首先在Co中找到反例，但F+G闭。正命题：B空间中子空间F，G一个可近。一个自反，F+G闭，F∩G有限维，则F+G可近，P．K．Lin1989年肯定了F∩G有限维条件可不需要。对F∪G，F∩G可近性等远远未有人研究。

对C(Q)，Q=S×T，S，T紧，1951年Diliberto－Strauss已确立C(S)+C(7)在C(SXT)中是可近集。这问题实即多元函数用较少元函数的组合最佳逼近存在性问题。进一步问，C(T)何时闭集G+H在C(S×T)可近?一般地G．Aumann1959年已造出反例。而Repess、Cheney 1980年研究正面结果是：当G，H是有限维子空间；到G，到H的度量投影一个连续，一个Lip的，则是C(S×T)中可近的余子空间。

与可近性研究同时，尚有两个问题，即双偶可近性(p．b．性，Proxbid)及极不可近性。前者即X在X^{* *}中可近性。

最早1960年J．Blatter的长文章论述C(Q)，Co，L¹(产)(μ正测度)都具p．b．性。1986年K．R．Davidson企图证明PAP(投影逼近性)空间X可以改等价范数使X于X^{* *}极不可近。

遗憾的是他那通过Co为线索的证明被王慕三和王建华1991年的文章指出错误，而且举出了反例。

不过改范数的研究日渐重视。

车氏集方面，1960年Phelps的对偶理论已涉及到。而实例空间，如C(Q)，L¹判定其中G车贝性有Singer1970年的书最详尽。

分G有限维、有限余维、及一般子空间逐一详尽，但显得琐碎。还有Garkavi工作。若结合空间条件，自反严凸空间中任意闭凸集是车氏集且此性质表征该类空间。利用对偶，知光滑空间表征，是比如1≤n≤dimX－1，n维任意的每个子空间具(U)性。

Singer推广到(k+1)严凸性则相应于k半车氏子空间(特别k=0)，O．Kroó1984年解决了C^γ［a，b］中n维G为车氏集的本征问题。在研究有限维G为车氏集时，1970年Ault、Deutsch、Morris和Olson引入内插子空间，它一定是车贝的，甚至强车贝的，而在C(Q)而言，正好是Haar条件。

车贝集一个根底问题是各种空间中，各种结构的车贝子空间(非平凡)是否存在?1956年着名的J．Maihuber定理指出C(Q)中存在维数n≥2的车贝子空间必须Q同胚于圆周一子集。所以C(［a，b］×［c，d］中n≥2维Haar组就不存在。

沿着M定理有1973年Henderson、Ummel考虑Q局紧情形。1982年Brown、1985年Mc Cullough、Wulbert给出了M定理的新证明。1964年Makovoz研究C(Q)中余维n车贝集存在条件，Phelps与Garkavi研究L1(μ)空间，竟在很常情况下，比如无原子，则n维车贝子空间不存在，除非有≥n个原子。余维n存在性恰好条件相同。

就L^∞(μ)而言，n维车贝子空间总是不存在，余维m都涉及有无≥m个原子。Singer1969和1974年建立两个例子，Co中的凡有限项以外为0的数列全体X₀，则X₀中不存在任何车贝子空间，但可分空间反例无人建立，存在众多未解决的问题。

B．空间是否必存在余维m的半车贝闭子空间?自反空间必存在余维m≥2的车贝或可近子空间吗?(自反空间必存在车贝超平面)。自反空间必存在一维车贝子空间吗?(若一维存在，2，3，……维必亦然)1970年Ewald、Larman和Roger指出若XN维，则低维车贝子空间必存在。

虽然通过Krein－Milman端点公式可推B．空间必存在半车贝闭超平面，但车贝超平面仍未解决。又空间什么本征，使有限维(或有限余维)车贝子空间存在?就C［a，b］中，是否存在无限维又是无限余维的车贝子空间亦未解决。1984年Sastry和Srinivasan研究存在的车贝超平面相应的ψ有多少，是否于S_x′中绸密。

着名车贝集凸性问题，至今未彻底解决。

最早1934年Bunt及Motzkin证出欧氏空间中车贝集必须是闭凸集，1961年Klee提出猜想Hilbert空间中车贝集可能必须是凸的或至少是太阳集，Vlasov1961年回答了B．空间中近紧车贝集必是太阳集，因而有限维空间中车贝集必是太阳集。

但仍未解决是否凸集，但加设了光滑空间则凸性肯定。1976年C．B．Dunham找到了C［0，1］中车贝集非太阳集。1987年G．Johnson找到了某实内积空间(非完备)中一个车贝集而非太阳集，故此，基本上否定了Klee猜想，但Hilbert空间如何，还未完全解决。

此外，Vlasov也获知光滑空间中的可近集，则太阳集等价于凸集。又1958年Efimov和Stechkin最早曾证明光滑空间中近紧车贝集是凸的，故此其全面推进Vlasov的工作。

Efimov和Stechkin(1963)首先研究殆(almost)车贝集G，即X到G有唯一佳逼元，这样x全体U_G是残集。

类似定义殆可近集。

对闭集(不设凸)逼近打开了研究的大门。他们(及1964年Garkavi)首先证明一致凸空间中凡闭集是殆车贝的，而(LUR)空间中闭集G，则U_G是稠密集。

1977年K．C．Lau的一系列工作改进到(LUR)兼自反空间中闭集是殆车贝的，而自反兼(H)空间中闭集是殆可近的。1976年M．Edelstein找到自反兼严凸空间中某闭集G却不是殆车贝的。改设(LUR)同样被否定。60年代Garkavi考虑C(Q)中的殆车贝集。1984年M．Bartele－D．Schmidt找到C(Q)中有限维子空间是殆车贝集的等价条件，用PGLip性表征之。1990年Schmidt研究了C(Q)中L′范数佳逼近的殆车贝集。

而“殆”方面工作已与P_G连续选，强唯一性等发生了联系。

。

【参考文献】：

1 Singer I. Best Approximation in Normed Linear Spaces by Elenents of Linear Subspaces, 1970

2 Blatter J. Mem,AMS, 1972,120:1 ～ 121

3 Singer I. The Theory of Best Approximation and Functional Analysis, SIAM,Philadelphia ,1974

4 Deutsch F. JAT ,1982,36:226～236

5 潘文熙．全国第3届逼近论会议论文集，南京大学版．1983，117～129

6 Deeb－R Khalil W．JAT 1989，59∶296～299

7 潘文熙．数学季刊，1989，4(2)∶39～48

8 矫恒利．数学研究与评论，1990，2∶221～226

9 李冲．数学学报，1990，62∶251～259

(暨南大学潘文熙教授撰)