观测值的改正和换算
出处:按学科分类—工业技术 中国建材工业出版社《工程测量实用技术手册》第425页(9813字)
测距仪所显示的斜距值由于各种测量误差的影响,都与实际斜距值有一些差异,为了求得两测点间的实际倾斜距离值,还要加入一些改正数。此外,为了工程上的需要,还要将斜距换算为水平距离,再将水平距离换算至平均海平面上和高斯投影面上的距离。下面所列的改正数项目和换算项目,并不是任何情况下都必须进行的,而是根据需要有选择地进行。目前,许多光电测距仪可通过内置程序自动计算以下改正:
1)气象改正数。由于观测时大气的折射系数(率)n不等于标准气象条件(也称仪器的气象参考点)下的大气折射系数而引起的。
2)波道弯曲改正数(也称曲率改正数)。由于光束在大气中弯曲传播所引起的。
3)调整头改正数。由于测距仪调整头基板不水平而引起的。
4)仪器和反射器加常数改正。由于测距仪和反射器的参考点与仪器和反射器中心(挂垂球处)不重合引起的。
5)测距仪和反射器归心改正数。由于仪器和反射器偏离测点标志中心而引起的。
6)倾斜距离改化为水平距离改正。
7)地面斜距改化为参考椭球面上的长度的改正。
8)参考椭球面上的长度化算为高斯投影面上的长度改正。
9)地面斜距改化为测区平均高程面的长度改正。
10)平均高程面上的长度改化为高斯投影面上的长度改正。
1.气象改正数
激光测距仪的气象改正,都是依据D=Ls(N+△N)来求解两测站点间的倾斜距离的。公式中的Ls值为Ls=c/(2nf)。可见,对于某仪器而言,其Ls值与光波传播路径上的大气折射系数n密切相关。大气折射系数(率)n又是随时间、地点、大气的温度t、压力p及湿度e的变化而变化的。研究证明n还与光波的波长λ有关,故Ls是t、p、及e的函数。对某种仪器而言,基本测尺频率的确定一般是在选定的标准气象(参考气象)条件下,用凑整的办法使对应的基本测尺长度等于方便计算的数值(一般为2.5m、5m、10m或20m),故仪器测得的斜距都是相应于标准气象条件下的斜距。然而测距时的实际气象条件一般不同于标准气象条件,为了求得实际气象条件下的斜距值,必须对测得的斜距值加入相应的改正数。
(1)基本公式
根据1963年召开的第十三届国际大地测量协会的决议,计算光速折射系数的公式有三个:
1)对于单色性好的激光而言,当未调制时,在标准气象条件下它的折射系数可按巴热尔-赛尔斯(Parrell-Sears)公式来计算:
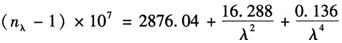
式中 λ——单色光的波长,单位为μm(1μm=10-6m);
标准气象条件:取p=760mmHg;t=0℃;水蒸汽压力e=0mmHg。
2)对于强度调制光而言,激光是以群速度传播的,故应采用群速度来求它在大气中传播时的折射系数ng。所谓群波速度就是不同波长光波速度的合成速度。在标准气象条件下,ng与nλ有如下关系:
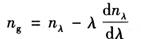
对巴热尔-赛尔斯公式求微分,则得:
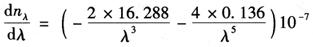
将上式代入式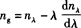 ,则得:
,则得:
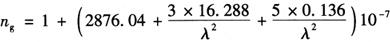
3)对于实际气象条件下,调制光在大气中传播时的折射系数n与ng又有如下关系:

式中 a=1/273.16=0.003661,称为空气膨胀系数;
p——实际的大气压力(mmHg);
t——实际的大气干温度(℃);
e——实际的水汽压力(mmHg)。
(2)实用算法波长为6.328×10-′m的氦氖气体激光测距仪的气象改正数△Dn的计算
1)这类仪器标准气象条件下折射系数ng的计算所用氦氖气体激光的波长λ=0.6328μm,将它代入上式,则得:
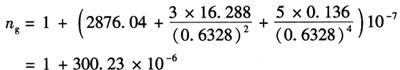
这就是DCX-30型等仪器所采用的基准折射系数n0=ng=1.00030023。
2)这类仪器实际气象条件下折射系数n。将ng值代入求n公式,可求得这类仪器在实际气象条件下的折射系数n为:
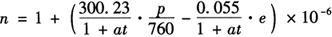
3)该类仪器所测距离的气象改正数△Dn的计算式。用电磁波测距的一般公式D=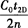 ,对n求微分得:
,对n求微分得:
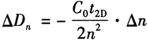
考虑到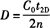 ,则上式可写成如下形式,得:
,则上式可写成如下形式,得:
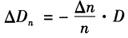
由于n≈1及△n=n-ng,所以上式又可写成如下形式,得:
△Dn=D(ng-n)
将ng=1+300.23×10-6及式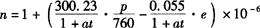 代入上式,则距离的气象改正数△Dn为:
代入上式,则距离的气象改正数△Dn为:
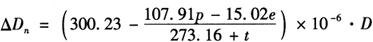
式中的p、e以mmHg(毫米汞柱)为单位,t以℃为单位计算。当式中的p及e以mb(毫巴)为单位时,由于1mmHg=1.33322368mb(反之1mb=0.75005mmHg),则上式又可写成如下形式:
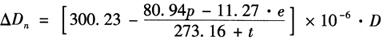
4)气象改正数△Dn的计算方法直接用上式计算,得:
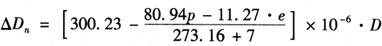
式中的p和t是根据观测时在测站与镜站测得的气象值求得平均值而取得的。e可以根据干温平均值p和湿温平均值t′求得。这类仪器目前的适用温度范围为-20~+40℃,此时水汽压可用下式计算:
e=E冰-0.000662(t-t′)·(1+0.001 146t′)p
式中 E冰——湿温为t′未结冰时的饱和水汽压,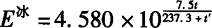 。
。
此外,e值也可由国家气象局编印的“湿度查找表”或仪器所附的“水汽压表”中查取。值得注意的是,由“湿度查找表”取得的e是以mb为单位的,因此应该用上式计算距离改正数△Dn。依气象测定值和上式求得p、t和e之后,代入式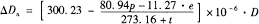 即可求得气象改正数△Dn。
即可求得气象改正数△Dn。
(3)短程红外测距仪气象改正数△Dn的计算
目前国内外短程红外测距仪由于所采用的光源的有效波长各不相同,故仪器的载波波长不一。各仪器所用载波的波长不同,选用的气象参考点也不相同,所以计算各仪器气象改正数的公式也有所不同。现将目前国内常见的几种仪器的气象改正数的计算方法简介如下:
距离气象改正数的计算式:
①标准气象条件下的折射系数ng的计算,将各波长值依次代入式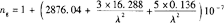 ,则得:
,则得:
a.载波波长为0.875μ的ng值为:ng=1+294.10×10-6;
b.载波波长为0.900μ的ng值为:ng=1+293.74×10-6;
c.载波波长为0.930μ的ng值为:ng=1+293.35×10-6。
②实际气象条件下的距离气象改正数△Dn的计算是将相应于各载波波长的ng及所选定的气象参考点,依次代入式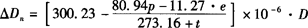 及式△Dn=D(n1-n),即可得到相应载波的距离气象改正数△Dn的计算式。
及式△Dn=D(n1-n),即可得到相应载波的距离气象改正数△Dn的计算式。
对于载波波长为0.875μm的仪器,选取的气象参考点为p=760mmHg、t=12℃、e=0mmHg。将ng=1+294.10×10-6及p、e、t值代入式,则得:
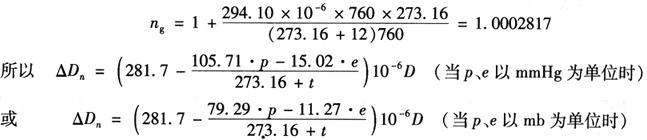
因一般情况下e《p,对于测程5km以下的短程测距仪可舍去含e项,则上两式可写成如下形式:
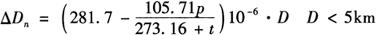
或
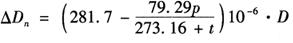
对于载波波长为0.900μm,参考点p=740mmHg,t=15℃仪器的距离气象改正数△Dn可依下式计算: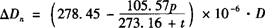 (当p以mmHg为单位时)
(当p以mmHg为单位时)
或

对于载波波长为0.930μm仪器时,其气象参考点为p=760mmHg,t=20℃,则距离的气象改正数△Dn应依下式计算:
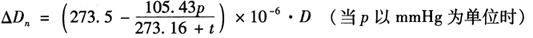
或
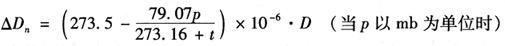
目前多数仪器已设有气象自动改正装置,故勿须对所测距离另加改正。有些仪器在运算电路或附带的计算器中进行比例因数运算,最后显示出经过气象改正后的距离值。例如,某仪器的专用计算器可使300m以内的距离自动进行归算,而不致影响本仪器的±5mm的测量精度。其做法是:测得的距离被显示之前,将比例因数开关置于相应位置(以p和t为引数,由所配卡片图查得相对应的开关挡位),则各种改正数(包括气象改正数、海平面归算及投影改化因数)自动进入计算器,最后显示的就是改正后的距离。这种自动改正法精度较低,但未超出仪器的测量精范围(±5mm)。当所测距离超过300m时,则应采用公式计算法或查图表法计算距离的气象改正数。
有的仪器内设置气象自动修正装置,把与温度t、气压p相对应的气象状态修正指数用开关分挡送入仪器,仪器即可自动调整测尺频率,以得到与实际气象条件相对应的测尺长度,因而此时测得的距离值即是经过气象改正后的距离值。
2.波道弯曲改正数△Dp
测距仪测得的距离应是仪器到反光镜的直线距离,但由于大气折射系数n是高度的函数,如图18-41所示,设大气由若干等指数球面组成,则光束从一个球面到下一个球面时将发生弯曲。测距仪光波的路径是弯曲的,其光路曲率与地球的半径R有关,光路半径约为8R。而且光路半径又随折光系数K的变化而变化。因此,测距仪测得的距离不是直线距离,而是曲线距离,所以测得的距离必须加两项改正。
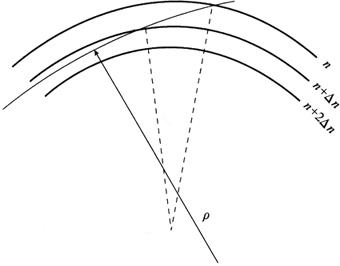
图18-41 波道弯曲
1)由于大气垂直折光影响而使光束路径呈向上弯曲的弧线,为将弧线改化成统长应加路径曲率改正,也称波道几何改正,或第一速度改正,用Hopeke教授推导出的公式,可表示为:
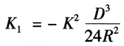
式中K——折光系数(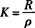 );
);
R——地球半径(R=6378km);
ρ——光束弧线曲率半径;
D——所测距离。
2)由于实际大气折光系数仅用测线两端所测定的气象参数的平均值代替沿线气象积分平均值,因而产生折射系数的代表性改正。其实质是沿测线光束传播速度变化的改正,也称为第二速度改正。用Hopeke教授推导的公式,可表示为:
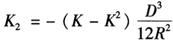
波道弯曲改正数(也称光束曲率改正数)△Dρ为上述两项改正数之和:
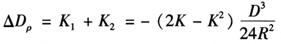
波道弯曲改正数△Dρ既可采用上式直接计算,也可采用预先编绘的图查找。图18-42为某仪器的改正数图,以D和K为引数查找。但无论是公式计算还是查图表,均需首先确定出垂直折光系数K的数值,而折光系数K随气候条件、地区和测线条件的不同而不同,因此要精确地求定K值是困难的。目前测定K值的方法有两种:其一是当已知测距仪和反光镜站间的高差时,可由单向观测垂直角来求K值;其二是根据两点间同时观测天顶距或垂直角的资料来求K值。解算K值的详细方法可参考《大地测量学》的有关内容。在直接测定K值不可能时,可参考表18-10所示的数值。

图18-42 波道弯曲改正图
表18-10 垂直折光系数K的数值

必须指出,这些数值仅是平均值,在特殊条件下,尤其当气候平稳而且光路贴近地面经过时,K值可能出现相当大的偏差。由图18-41可知,当距离小于20km时,波道弯曲改正数几乎为零(小于10km△Dρ即为零),故短程测距不加此项改正数。
3.仪器加常数改正K
由于测距仪的发射中心、接收中心与仪器的置中(对中)轴线不在和测线相垂直的同一铅垂面内,以及反光镜的偏心等因素的影响,使得仪器测距时的光程不等于被测距离的两倍,因而用仪器测得的距离值与距离的实际值之间有一差数,此差数称仪器加常数。如图18-43所示,设D为被测距离,La为光在测线上往返所走过的路程(光程),Li为光在内光路系统的有效光程,Lr为光在反射镜内入射、反射折合到空气中的有效光程。由前述可知,外光路测量时的相位移φ0l=2La+Lr,而内光路测量时的相位移φi=Li,由于(2La+LrLi)不一定等于2D,故内光路测量相位移之差(φ0l-φi)=Φ′不一定等于光径两倍距离所产生的相位移Φ。因此,由测距仪测得的距离值与距离实际值有一固定差值,它称为仪器加常数。实际上,这一差值中包括了测距仪的加常数和反射器的加常数,在短程测距中这两项常数合称为仪器加常数,而在长程测距仪中,则常将两者分开,以便作业中不同测距仪和反射器间的互配使用。不同类型的测距仪,其仪器加常数是不相同的,即是同一型号的仪器,各台之间加常数也往往不一样。所以仪器出厂前要精确地测定其加常数,以便进行此项改正。
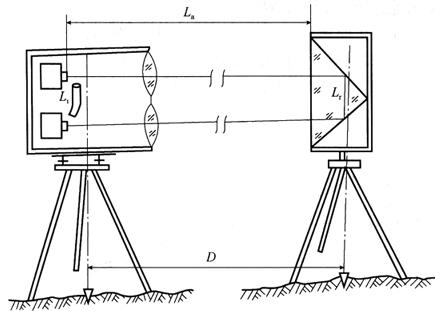
图18-43 测距仪加常数
加常数的测定方法:在已知的高精度短基线上进行测距,将改正(气象、周期误差等改正)后的观测值与基线值之差的平均值作为仪器的加常数K,即为:

式中D0——已知基线的长度;
Di——仪器的观测值(经改正后的);
n——为观测的次数。
由于仪器常数K要对每条测线的观测成果进行改正,故仪器常数的测定误差必将影响所有的距离观测成果。为了提高仪器加常数的测定精度,通常可采用以下措施:其一是对中、长程测距仪而言,已知基线要尽量缩短,目前多在数百米或1~2km的短基线上进行,以减小或消除气象代表性误差。对于短程测距仪而言,一般应在400~600m的短基线上进行,一般认为这是短程测距仪的最佳测程;其二是增加观测的时间段和测回数,以减弱或消除各种误差的影响,提高测定精度。目前国产DCX-30型测距仪采用的时间段为6个(即白天3个,晚上3个),每个时间段测4组成果,每组3个测回(即用f1、f2、f3等3个测尺频率各测一个测回)。
仪器加常数的改正方法有如下三种:
1)由测量人员在整理测量记录的过程中加入仪器常数K,此法主要用于自动化程度不高的中、长程测距仪测量成果的计算。
2)由测量人员在进行测距的过程中加入仪器加常数。如早期威尔特测距仪,用望远镜瞄准反光镜之后,转动控制箱面板上的CAL旋钮,把细度盘读数放置到CAL值上。此操作即是为了加入仪器加常数。
3)在自动数字法测距仪中,仪器能在测量前后自动加入仪器常数改正,故显示的距离值已经加入了仪器常数改正,这种方法称自动预置仪器常数,较为先进的短程测距仪一般都采用预置加常数方法,用户不再考虑此项改正。
4.测距仪和反光镜的归心改正数△De
高精度测距,有时存在偏离标石中心设站进行偏心观测,这时则应加入归心改正数△De。如图18-44所示,设A、B为标石中心点,A′、B′为偏心观测的测站点,e1、e2为偏心距,θ1、θ2为偏心角(以测站点为中心,从偏心距顺时针量至测线方向的角度),实测的距离为D,标石中心间的距离为D1,则归心改正数△De=D1-D。现将△De的计算公式推导如下。
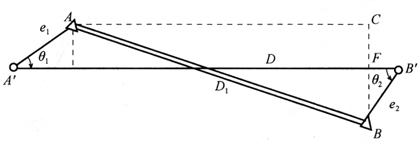
图18-44 归心改正
在图18-44中,作直线AC平行于A′B′的垂线与A′B′交于E,过B点作A′B′垂线BC且交于F。从图中可以看出:
AC=A′B′-A′E-B′F
而 A′E=e1cosθ1 及B′F=e2cosθ2
AC=D-(e1cosθ1+Cosθ2)
在直角三角形ABC中:
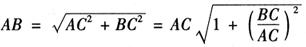
由于AC》BC,则上式可按级数展开,当仅取一次项时,则得:
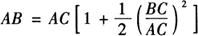
设以观测值D代替上式第二项中的AC时得:
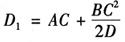
因为 BC=CF+BF=e1cosθ1+e2cosθ2
所以
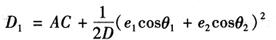
将AC=D-(e1cosθ1+cosθ2)代入上式,可得归心改正数的计算式为:
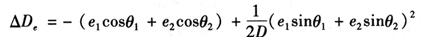
当偏心距不大时[即当(e1+e2)(以米为单位)<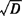 (以公里为单位)时],可略去上式的第二项,归心改正数算式可简化为:
(以公里为单位)时],可略去上式的第二项,归心改正数算式可简化为:
△De=-(e1cosθ1+e2cosθ2)
5.斜距的总改正数△D
综合前述,斜距的总改正数△D为:
△D=△Dn+△Dρ+△Da+K+△De
斜距的正确值D0则为:
D0=D+△D=D+△Dn+△Dρ+△Da+△De+K
现对上式讨论如下:
1)对于中、长程测距仪而言,由于所测距离一般较长(数公里以上),上述几项改正数一般都不可缺少。
2)短程测距仪测程较短(数十米至几公里),波道弯曲改正为零;又因一般测量时勿须偏心设站,故△De=0。
3)调整头改正数△De用于有专用机座的中长程测距仪。专用机座主要用于补偿三角架头不平引起的基板不平,但调整头自动置平一般会引起测距仪参考点偏心。此项改正一般很小。
4)仪器的照准头一般都安装在经纬仪的望远镜上,或安置在特制的机座上。测距时是从照准头而不是从望远镜横轴测量的;即从图18-45可见,是以距离D代替D1,因此又产生了照准头偏心的改正数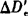 。
。
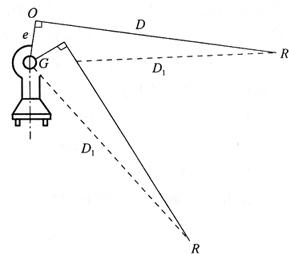
图18-45 照准头偏心改正
设照准头的偏心距为e,当用T2仪器时,e=90mm,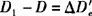 。
。
由直角三角形GOR得:
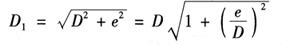
将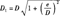 展成级数形式,且只取一次项,则得:
展成级数形式,且只取一次项,则得:
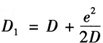
从而可求得偏心改正数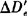 ,为:
,为:
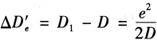
若D=4m,e=100mm,代入上式则得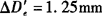 。距离越长,
。距离越长,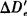 越小,一般可以不考虑e的影响。此外,由图18-44可以看出,
越小,一般可以不考虑e的影响。此外,由图18-44可以看出,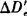 的大小与视线倾斜角β无关。总之,对短程测距仪而言,斜距的改正一般只考虑气象改正这一项(因仪器常数可预置)。
的大小与视线倾斜角β无关。总之,对短程测距仪而言,斜距的改正一般只考虑气象改正这一项(因仪器常数可预置)。
由此可见,依式D0=D+△D=D+△Dn+△Dρ+△Da+△De+K进行斜距改正计算时,加某项改正数要具体情况具体分析,即主要依据它的影响程度大小而定。
6.距离的换算
由于地形测图及工程测量所需要的点位坐标是平面坐标,而我们的测距工作又是在地球表面进行的。为此需进行测距成果的换算,主要包括两步换算:
1)将地面距离换算为参考椭球体面(基准面)上的距离。对小范围控制区或施工区而言,则是将地面距离换算为该地区的平均高程面上的距离。
2)将参考椭球体面(或平均高程面)上的距离换算为高斯投影平面上的距离。
这些换算的计算公式和计算方法在有关的《大地测量学》或《控制测量学》等书籍中都有详细的介绍,故此不赘述。