非电量的测量
出处：按学科分类—工业技术 江苏科学技术出版社《简明电工计算手册》第365页（22154字）
1．温标
物体的冷热程度用温度表示，温度不能直接测量，只能借助于物体的某些物理参数随温度变化的特性来间接测量。通常温度用华氏、摄氏和国际实用温标来表示。
(1)华氏温标
华氏温标用符号t′表示，单位为华氏度，用符号℉表示。
华氏温标是将水的冰点和沸点之间的温度差分为180等份，每一等份为华氏一度。
规定水的冰点温度值为32℉，沸点为212℉。
(2)摄氏温标
摄氏温标用符号t表示，单位为摄氏度，用符号℃表示。
摄氏温标是将水的冰点和沸点之间的温度差分为100等份，每－等份为摄氏一度。
规定水的冰点温度值为0℃，沸点为100℃。
华－摄换算关系为：
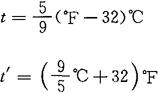
［例4－10］ 摄氏0度及摄氏100度分别合多少华氏度?
(3)国际实用温标
“国际实用温标－1968”简称“IPTS－68”，规定温度可由摄氏温标或凯氏温标两种温标表示。
凯氏温标是一种绝对温标，规定分子运动停止时的温度为绝对零度或最低理论温度。
凯氏温标用符号T表示，单位为凯尔文，用符号K表示。
摄－凯换算关系为：
t=T－T0
式中 T0=273．15K；
t——摄氏温度数；
T——凯氏温度数。
［例4－11］ 水的冰点及沸点分别是0℃及100℃。若用凯氏温标表示，则分别为多少度?两种温标的温度差各是多少?
［解］ T=t+T0=0+273．5=273．15(K)
T′=t+T0=100+273．5=373．15(K)
△T=T′－T=373．5－273．5=100(K)
△t=t′－t=100－0=100(℃)
2．热电阻测温
工业上广泛应用热电阻测量“－200～500℃”的低温和中温。这是因为热电阻具有工作稳定，测量精度高，便于远距离传输信号，容易实现自动测量等优点。
目前常用的热电阻是铂电阻和铜电阻。
(1)铂电阻
铂电阻的温度与电阻关系可用下列两式计算：
0～6340．74℃范围内为：
Rt=R0(1+At+Bt2)
－190～0℃范围内为：
Rt=R0［1+At+Bt2+C(t－100)t3］
式中 Rt——温度为t℃时的电阻值(Ω)；
R0——温度为0℃时的电阻值(Ω)；A，B，C——常数，由实验方法求得：
A=3．96847×10－3(℃－1)
B=－5．847×10－7(℃－2)
C=－4．22×10－12(℃－4)
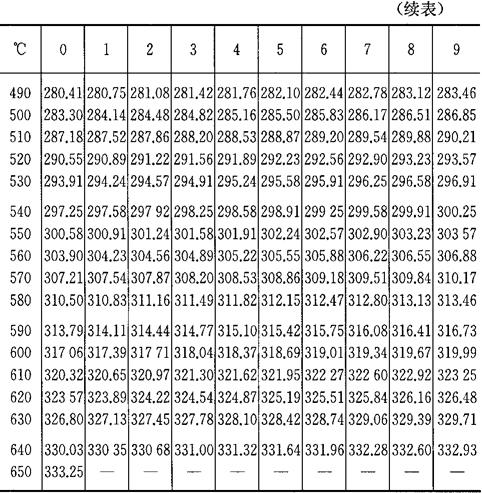
由上式得知要确定电阻Rt与温度t的关系时，首先要确定R0的数值。R0不同时，Rt与t的关系也不同，这种Rt－t的关系称为分度表，用分度号来表示。表4－3，表4－4为铂电阻的分度表。在实际测量中，只要测得铂热电阻的阻值Rt，便可以从分度表中查出对应的温度值。
表4－3 铂热电阻分度表(R0=46Ω)
R0=46．00Ω分度号：BA1
A=3．96847×10－3℃－1
B=－5．847×10－7℃－2
C=－4．22×10－12℃－4－200～650℃的电阻对照
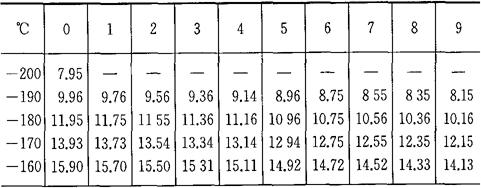
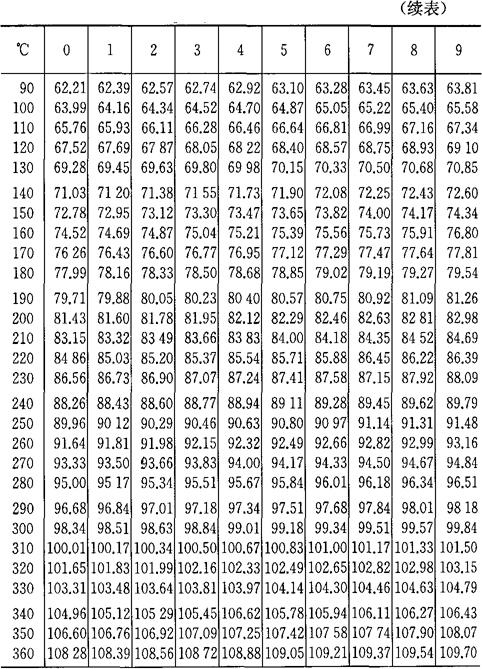
表4－4 铂热电阻分度表(R0=100Ω)
R0=100．00Ω分度号：BA2
A=3．96847×10－3℃－1
B=－5．847×10－7℃－2
C=－4．22×10－12℃－4－200～650℃的电阻对照
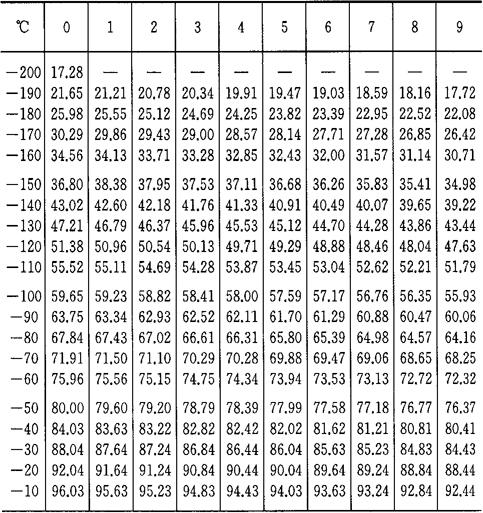
(2)铜电阻
铜电阻的阻值与温度的关系几乎是线性的，电阻温度系数α比较大，材料容易提纯，更重要的是铜电阻的价格比铂电阻便宜得多。所以铜电阻被广泛用于－50～150℃范围内的温度测量。
铜电阻的温度与电阻的关系可用下式计算：
Rt=R0 (1+αt)
式中 Rt——温度为t℃时的电阻值(Ω)；
R0——温度为0℃时的电阻值(Ω)；
α——铜电阻的电阻温度系数(0℃时，α=4．25×10－3／℃)。
表4－5，表4－6为铜电阻分度表。在实际测量中，只要测得铜热电阻的阻值Rt，便可以从分度表中查出对应的温度值。
表4－5 铜热电阻分度表(R0=50Ω)
R0=50．00Ω 分度表：Cu50－50～150℃的电阻对照
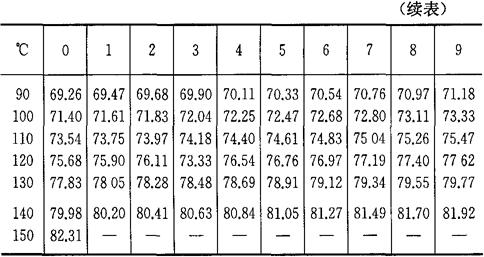
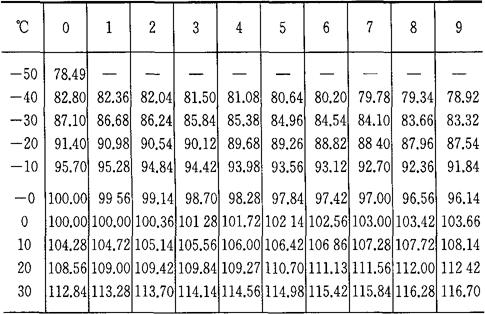
表4－6 铜热电阻分度表(R0=100Ω)
R0=100．00Ω 分度表：Cu100－50～150℃的电阻对照
3．热电偶测温
热电偶是将温度转换成电势的热电式传感器。
(1)热电效应
热电偶的基本工作原理是基于物体的热电效应。由两种不同材料的导体A和B组成闭合回路如图4－17所示，当两个结点温度不同时，回路中将产生电势。这种现象即称为热电效应或称塞贝克效应。
图4－17 热电偶原理图
两种不同材料的导体组成的回路叫热电偶。组成热电偶的导体叫热电极。热电偶所产生的电势叫热电势。热电偶的两个结点中，置于温度为T的被测对象中的结点叫测量端，又叫工作端或热端；置于参考温度为T0的另一个结点叫参考端，又叫自由端或冷端。
热电偶产生的热电势EAB(T，T0)由接触电势和温差电势两部分组成。如图4－18所示。
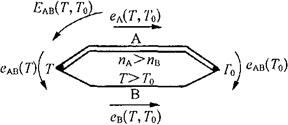
图4－18 热电偶的热电动势
接触电势(又称珀尔帖电势)是由于两种不同导体的自由电子密度不同而在接触处形成的电势。它的数值取决于两种导体的性质和接触点的温度，而与导体的形状及尺寸无关。即：
式中 eAB(T)——A、B两种材料在温度为T时的接触电势；
T——接触处的绝对温度；
k——波尔兹曼常数(k=1．38×10－23J／K)；
e——电子电荷(e=1．6×10－19C)；
nA、nB——热电极材料A、B的自由电子密度。
温差电势(又称汤姆逊电势)是在同一根导体中，由于两端温度不同而产生的一种电势。若A导体两端的温度分别为T、T0时，温差电势eA(T，T0)可由下式求得：
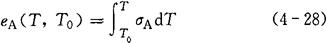
式中 σA——A导体的汤姆逊系数。
热电偶回路中起主要作用的是两个结点的接触电势。如果将单一导体的温差电势eA(T，T0)和eB(T，T0)忽略不计，则有
由上式得知热电势的大小只与材料和结点温度有关，与热电偶的尺寸形状无关。
(2)热电偶定律
①中间导体定律。若在热电偶回路中插入中间导体，只要中间导体两端温度相同，则对热电偶回路的总热电势无影响。即中间导体定律。证明如下：
如图4－19所示，热电偶回路插入中间导体C后的热电
势为
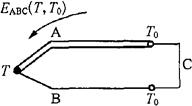
图4－19 具有中间导体的热电偶回路
EABC(T，T0)=eAB(T)+eBC(T0)+eCA(T0)因为
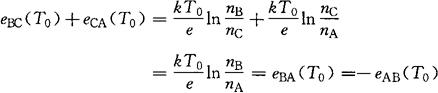
所以
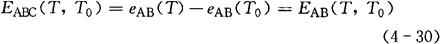
同理，热电偶回路中插入多种导体后，只要保证插入的每种导体的两端温度相同，则对热电偶的热电势也没有影响。
利用热电偶来实际测温时，连接导线和显示仪表等均视为中间导体，只要保证中间导体两端温度相同，则对热电偶的热电势没有影响。
②参考电极定律(也称组成定律)。如图4－20所示，已知热电极A、B与参考电极C组成的热电偶在结点温度为(T，T0)时的热电势分别为EAC(T，T0)、EBC(T，T0)，则在相同温度下，由A、B两种热电极配对后的热电势EAB(T，T0)可由下式计算：
图4－20 参考电极回路
EAB(T，T0)=EAC(T，T0)－EBC(T，T0) (4－31)
当结点温度采用摄氏温度t来表示时(t=T－273．15K)，则式(4－31)可写成：
EAB(t，t0)=EAC(t，t0)－EBC(t，t0) (4－32)
参考电极定律大大简化了热电偶的选配工作。只要我们获得有关热电极与参考电极配对的热电势，那么任何两种热电极配对时的热电势可按式(4－32)求得，而不需逐个进行测定。
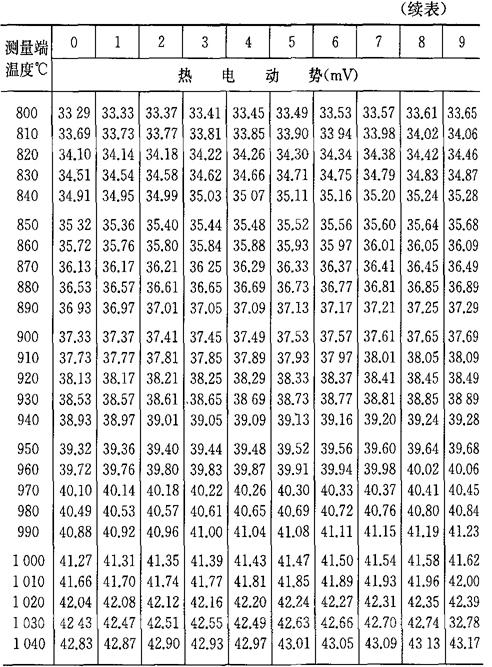
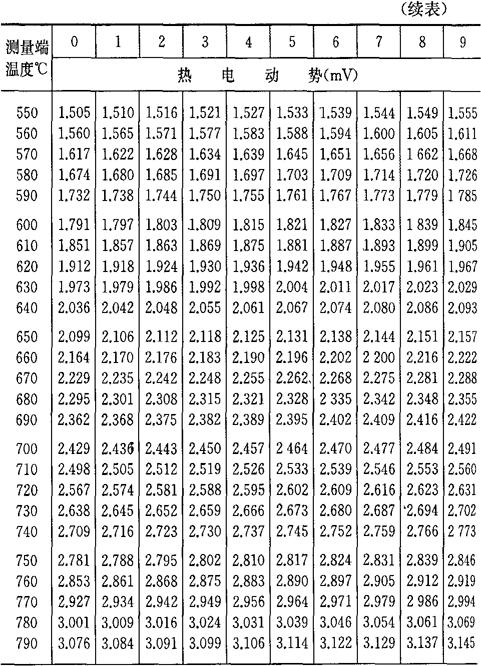
［例4－12］ 已知铂铑30－铂热电偶的E(1084．5℃，0℃)=13．976mV，铂铑6－铂热电偶的E(1084．5℃，0℃)=8．354mV，求铂铑30－铂铑6热电偶在同样温度时的热电势。
［解］ 设A为铂铑30电极，B为铂铑6电极，C为纯铂电极。已知t=1084．5℃，t0=0℃，则利用式(4－32)可求得
EAB(1084．5℃，0℃)=EAC(1084．5℃，0℃)－EBC(1084．5℃，0℃)
=(13．976－8．354)mV
=5．622mV
③中间温度定律。如图4－21所示，热电偶在结点温度为t，t0时的热电势EAB(t，t0)等于该热电偶在(t，tn)及(tn，t0)时的热电势EAB(t，tn)与EAB(tn，t0)之和。这就是中间温度定律，其中tn称为中间温度。它可用下式表示：
图4－21 存在中间接点的热电偶回路
EAB(t，t0)=EAB(t，tn)+EAB(tn，t0) (4－33)
中间温度定律的实用价值在于：
a．热电偶中补偿导线的使用依据了中间温度定律。补偿导线是指在一定温度范围内(0℃～100℃)，其热电性能与相应热电偶的热电性能相同的廉价导线。在图4－21中，若与热电极A、B相连的A′、B′为该热电偶的补偿导线，根据补偿导线的定义有
EA′B′(tn，t0)=EAB(tn，t0) (4－34)
所以可以把接补偿导线后的热电偶回路看作仅由热电极A、B组成的回路，只是自由端已由tn延伸到t0处了。
必须指出，使用补偿导线仅能延长热电偶的自由端，而不起任何温度补偿作用，将其称为“补偿导线”是名不副实的习惯用语。
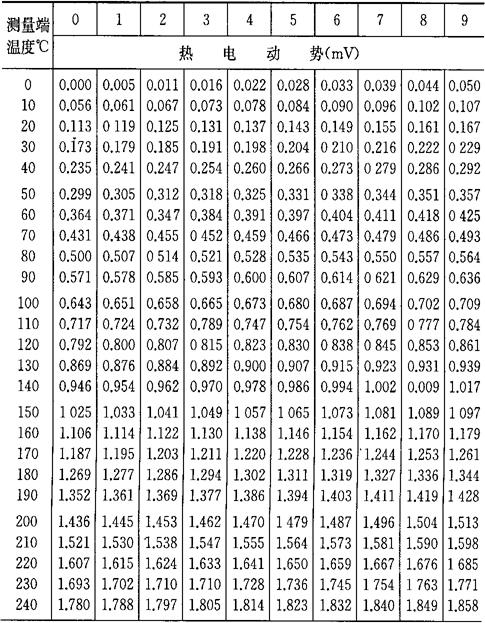
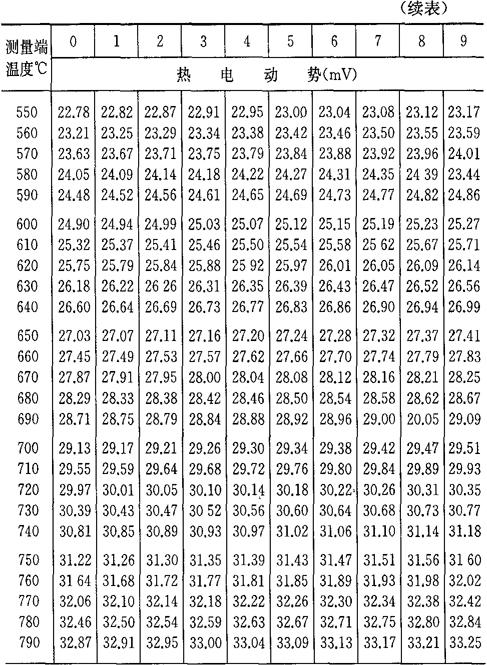
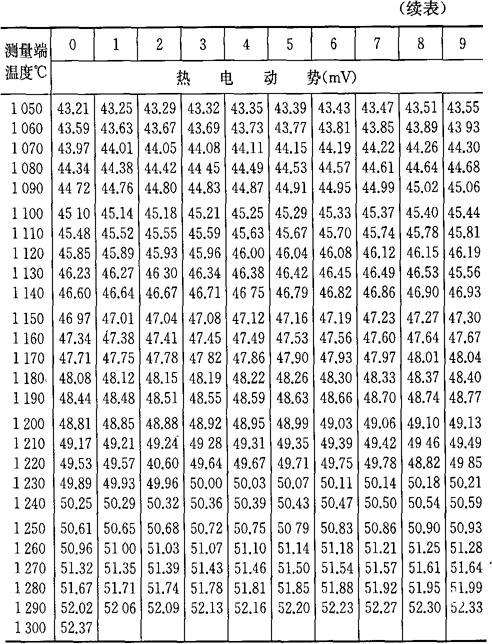
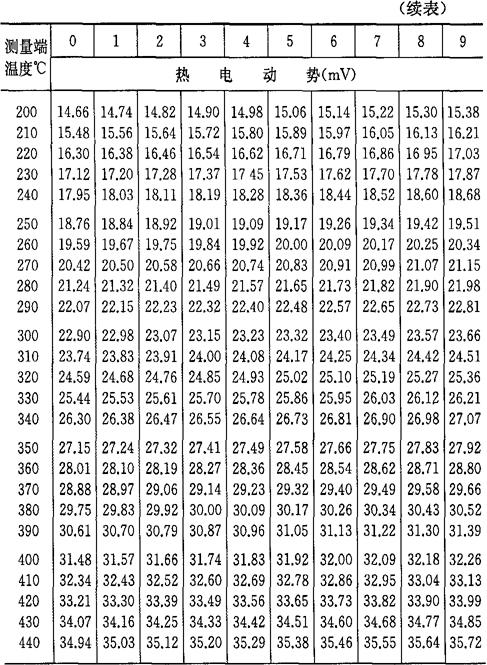
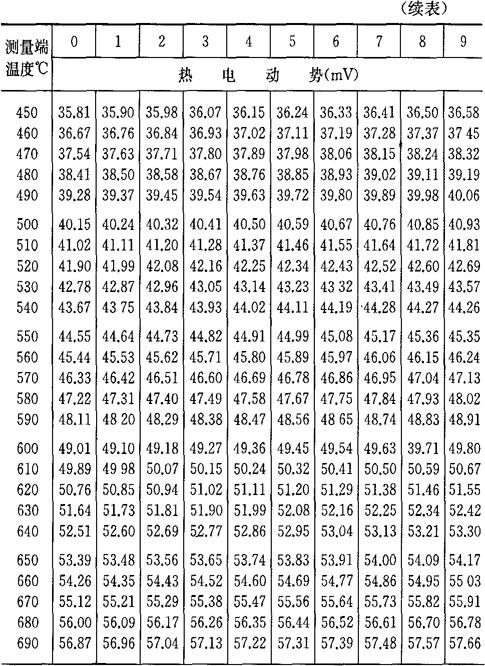
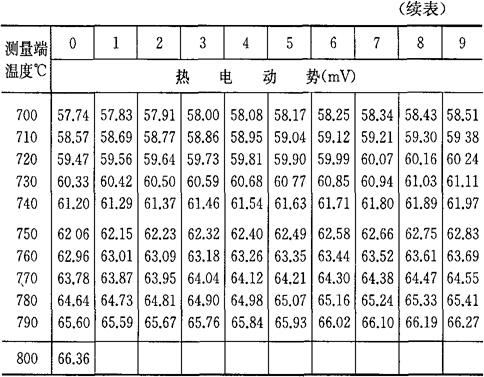
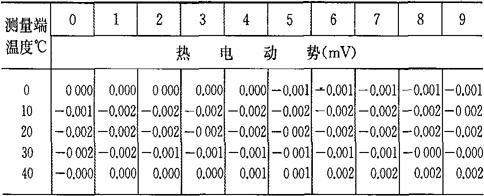
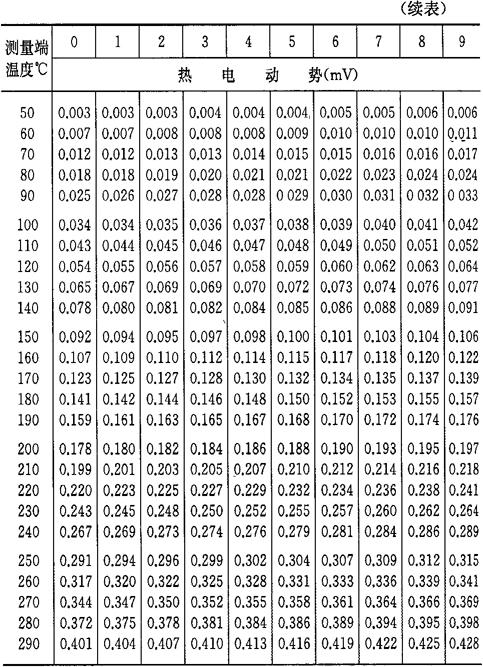
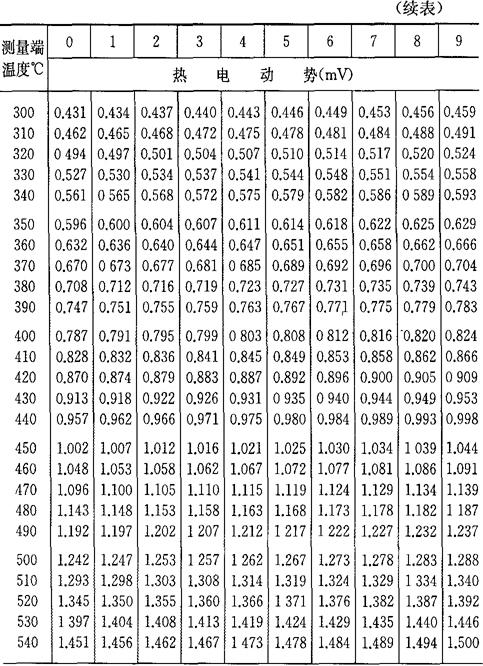
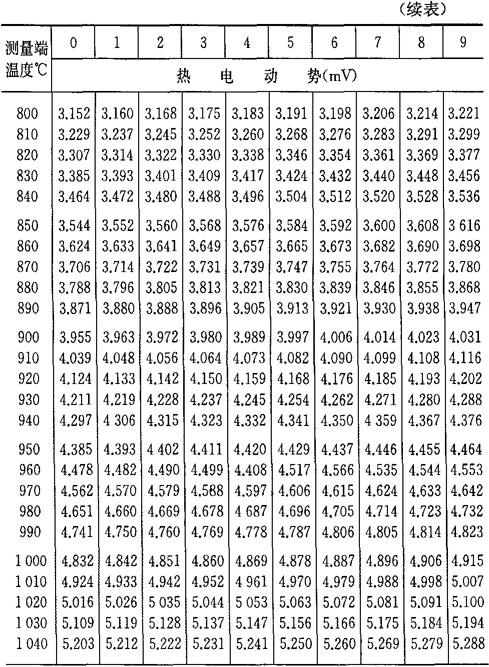
b．当自由端温度为0℃时，将热电偶工作端温度与热电势的对应关系列成热电偶的分度表，如表4－7～表4－10所示。如果自由端温度不为0℃，则可通过式(4－33)及分度表求得工作端温度t。
［例4－13］ 用一支铂铑10－铂热电偶测量某一温度，已知参考端温度为20℃，测得热电势为8．421mV，求被测温度t。
［解］ 由表4－7查得
E(20℃，0℃)=0．113mV
由式(4－33)得
E(t，0℃)=E(t，20℃)+E(20℃，0℃)=8．421+0．113
=8．534(mV)
再由表4－7查得
E(910℃，0℃)=8．534mV
所以被测温度为
t=910℃
表4－7 铂铑10－铂热电偶分度表
(参考端温度为0℃)分度号S
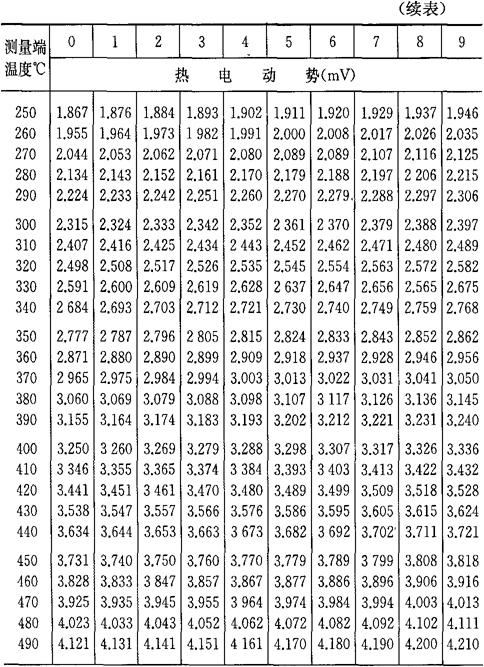
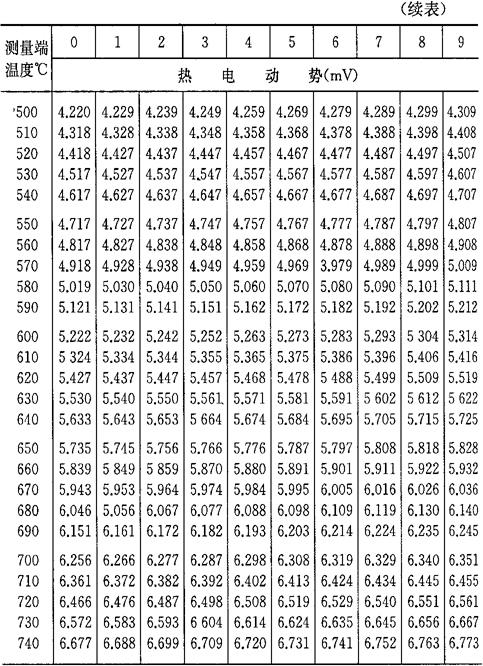
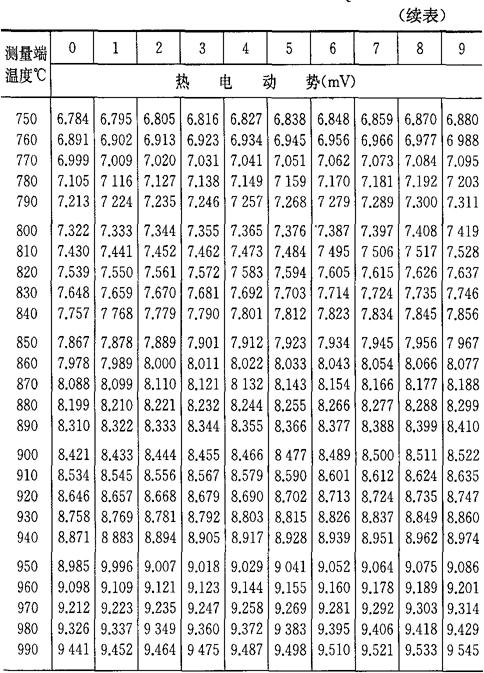
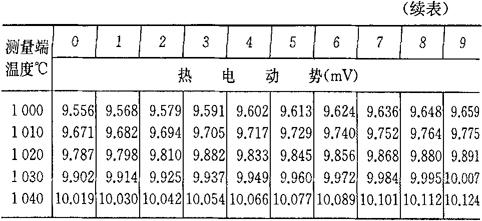
注：根据“国际实用温标－1968”修正。
表4－8 镍铬－镍硅(镍铝)热电偶分度表
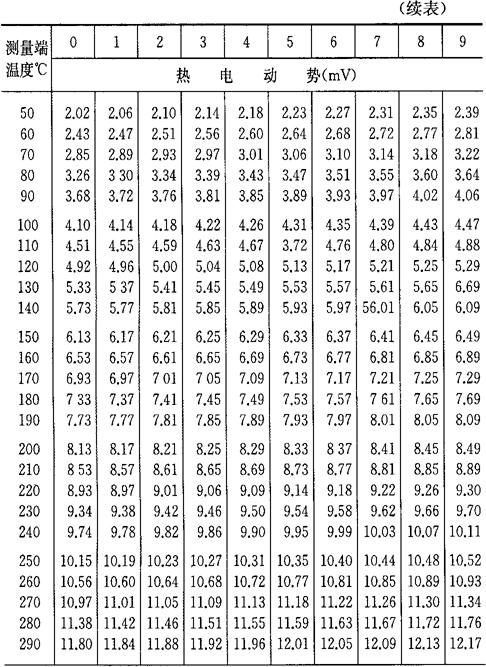
注：根据“国际实用温标－1968”修正。
表4－9 镍铬－考铜热电偶分度表
注：根据“国际实用温标－1968”修正。
表4－10 铂铑30－铂铑6热电偶分度表
(参考端温度为0℃)分度号B
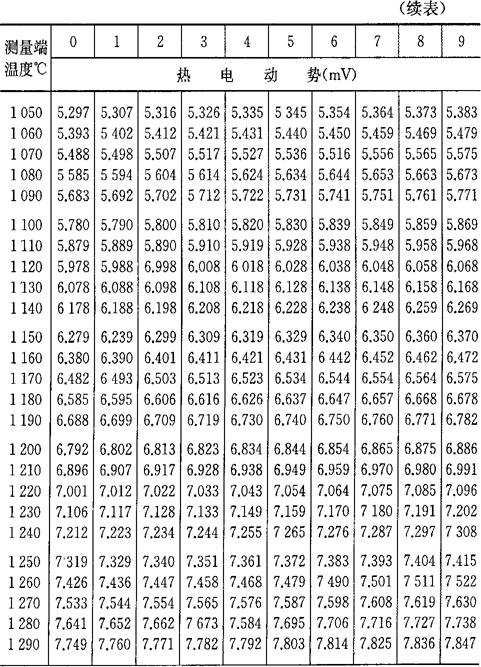
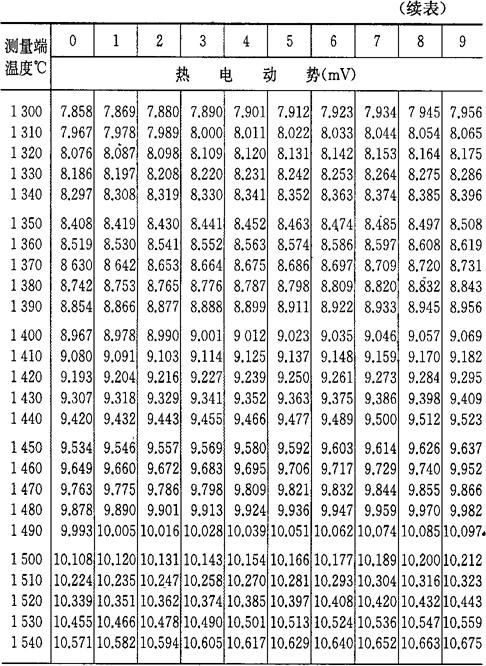
注：根据“国际实用温标－1968”修正。
参考数据：温度(℃) －20 －40 电热动势(mV) 0006 0022
4．高温比色温度计测温
图4－22为高温比色温度计原理图。其各部分的作用如下：
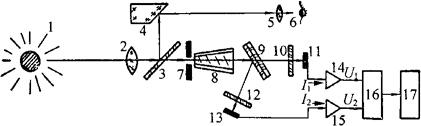
图4－22 高温比色温度计原理图
1－测温对象 2－物镜 3－半反半透镜 4－反射镜 5－目镜 6－观察者的眼睛 7－光阑 8－光导棒 9－分光镜 10、12－滤光片 11、13－硅光电池 14、15－电流／电压变换器 16－运算电路 17－显示器
1－测温对象(产生光辐射)→2－物镜(聚焦)→3－半反半透镜(反光及透光)→4－反射镜(反光)→5－目镜(聚焦)→6－眼睛(观测)
7－光阑(控制光通量)→8－光导棒(混合均匀)→9－分光镜(红外光透射进入10，可见光反射进入12)
－滤光片(得波长λ1的红外光)→11－硅光电池(将辐射强度Iλ1成正比地转换成光电流I1)→14－电流／电压转换器(将光电流I1转换为电压U1)－△。x→12－滤光片(得波长λ2的可见光)→13－硅光电池(将辐射强度Iλ2成正比地转换成光电流I2)→15－电流／电压转换器(将光电流I2转换为电压U2)－△→16－运算电路(U1／U2=Iλ1／Iλ2=K1e－K2／T计算出被测温度T)→17－显示器(反映被测物的温度)。
高温比色温度计根据辐射定律，使用光电池进行非接触测温。
根据辐射定律，物体在两个特定波长λ1、λ2上的辐射强度Iλ1、Iλ2之比与该物体的温度成指数关系：
Iλ1／Iλ2=K1e－K2／T (4－35)
式中 Iλ1、Iλ2——辐射强度；
K1、K2——与λ1、λ2及物体的黑度有关的常数；
T——温度。
因此只要测出Iλ1与Iλ2之比，就可根据上式算得物体的温度T。
5．压电式传感器
压电式传感器是一种典型的自发式传感器。它以某些电介质的压电效应为基础，在外力作用下，在电介质的表面产生电荷，从而实现非电量电测的目的。压电式传感器用于力、压力、加速度等的测量。
(1)压电效应
某些物质在沿一定方向受到外力作用而发生变形时，内部会产生极化现象，同时在其表面产生电荷，当外力去掉后，又重新回到不带电的状态。这种现象称为压电效应。
反之在其极化方向施加交变电场，它会产生机械变形，当去掉外加电场，其变形随之消失。这种现象称为逆压电效应(电致伸缩效应)。把具有压电效应的物体称为压电材料或压电元件。常见的压电材料有石英、钛酸钡、锆钛酸铅等。
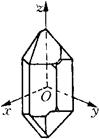
(2)石英晶体的压电效应
图4－23为天然结构的石英晶体，它是个六角形晶柱。在直角坐标系中，z轴表示其纵向轴，称为光轴；x轴平行于正六面体的棱线，称为电轴；y轴垂直于正六面体棱面，称为机械轴。
(a)石英晶体
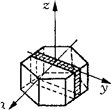
(b)石英晶片的割取
图4－23 石英晶体
通常把沿电轴(x轴)方向的力作用下产生电荷的压电效应称为“纵向压电效应”；
而把沿机械(y轴)方向的力作用下产生电荷的压电效应称为“横向压电效应”；
光轴(z轴)方向受力时，不产生压电效应。
石英晶体切片如图4－24所示，其长度、宽度、厚度分别为l、b、δ。
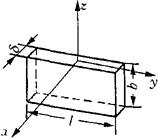
图4－24 石英晶体切片
当沿电轴(x轴)方向施加作用力Fx时，则在与电轴垂直的平面上产生电荷Q，其大小为：
Q=d11·Fx (4－36)
式中 Q——电荷量(C)；
Fx——沿电轴方向施加的作用力(N)；
d11——x轴方向受力时的压电系数(d11=2．31×10－12C／N)。
由上式得知，切片上产生的电荷量Q正比于作用力Fx，而与晶体切片的几何尺寸无关。电荷量Q的正、负符号视Fx是受压还是受拉而决定。
当沿机械轴(y轴)方向施加作用力Fy时，则在与电轴垂直的平面上产生电荷Q，其大小为：
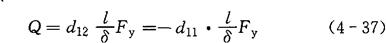
式中 Q——电荷量(C)；
l、δ——晶体切片的长度和厚度；
Fy——沿机械轴(y轴)施加的作用力(N)；
d12——y轴方向受力时的压电系数，石英轴对称，d12=－d11。
由上式得知，沿机械轴(y轴)方向的力作用在晶体切片上产生的电荷量与晶体切片的几何尺寸有关。式中的负号说明沿y轴的压力所引起的电荷极性与沿x轴的压力所引起的电荷极性是相反的。
(3)压电元件的等效电路
压电元件在承受沿其敏感轴方向的外力作用时，就产生电荷，因此它相当于一个电荷发生器，当压电元件表面聚集电荷时，它又相当于一个以压电材料为介质的电容器，其电容值Ca为：
式中 Ca——等效电容(F)；
A——压电元件电极面面积(m2)；
δ——压电元件的厚度(m)；
ε0——真空介电常数(ε0=8．85×10－12F／m)；
εr——压电材料的相对介电常数，随材料不同而变。
因此可以把压电元件等效一个电荷源与一个电容相并联的电荷等效电路，如图4－25(a)所示。
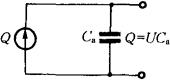
(a)电荷等效电路
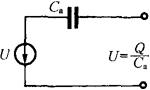
(b)电压等效电路
图4－25 压电式传感器的等效电路
压电元件也可以等为一个电压源和一个串联电容表示的电压等效电路，如图4－25(b)所示。
压电元件与二次仪表配套使用时，其完整的等效电路还包括连接电缆的等效电容Cc，放大器的输入电阻R1，输入电容C1及压电元件的漏电阻Ra等。
由于外力作用在压电元件上产生的电荷只有在无泄漏的情况下才能保存，即需要测量回路具有无限大的输入阻抗，这实际上是不可能的，因此压电式传感器不能用于静态测量。
压电元件在交变力的作用下，电荷可以不断补充，供给测量回路以一定的电流，故只适用于动态测量。
(4)压电传感器的测量电路
压电式传感器的输出信号非常弱，且内阻抗极高，需要与高输入阻抗的前置放大器配合，然后再采用一般的放大、检波、显示、记录电路。目前普遍使用电荷前置放大器，如图4－26所示。
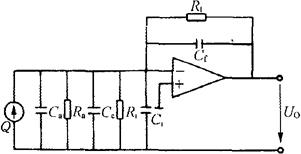
图4－26 电荷放大器等效电路
电荷前置放大器是一个具有反馈电容Cf的高增益运算放大器电路。当放大器开环增益A和输入电阻，反馈电阻相当大时，放大器的输出电压Uo正比于输入电荷Q，即：
式中 Uo——放大器输出电压(V)；
Q——电荷量(C)；
Cf——反馈电容(F)。
由上式得知，电荷放大器的输出电压仅与输入电荷量和反馈电容有关，电缆电容等其他因素的影响可忽略不计。
(5)压电式加速度传感器
压电式加速度传感器原理如图4－27(a)所示，当传感器与被测加速度的机件紧固在一起后，传感器受机件运动的加速度作用，惯性质量块产生惯性力，其方向与加速度方向相反，大小由F=ma决定。以惯性力作用在压电晶片上，产生电荷，电荷由引出电极输出，由此将加速度转换为电荷。弹簧是给压电晶片施加预紧力的。图4－27(b)为压电加速度传感器的结构图。
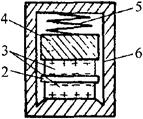
(a)原理图
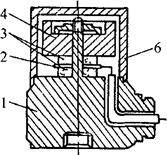
(b)传感器结构
图4－27 压电式加速度传感器
1－基座 2－引出电极 3－压电晶片 4－质量块 5－弹簧 6－壳体
压电式加速度传感器的灵敏度：
传感器有电荷灵敏度Sq和电压灵敏度Sv两种表示法，其一般表达式为：
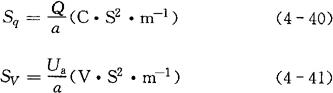
式中 Sq——电荷灵敏度(C·S2·m－1)；
SV——电压灵敏度(V·S2·m－1)；
Q——电荷量(C)；
a—加速度(m·s－2)；
Ua——传感器开路电压(V)。
［例4－14］ 用压电式加速度传感器和电荷放大器测量一机器的振动，已知传感器的灵敏度为100pC／g，电荷放大器的反馈电容Cf=0．001μF，测得输出电压峰值Uom=0．4V，石英晶片的压电系数d11=2．3×10－12C／N。求机器振动加速度的最大值am及石英晶片上的承受力Fx。
［解］ 由式(4－39)求电荷量Q
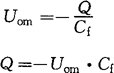
由式(4－40)求加速度am。
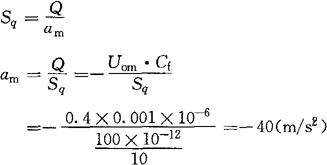
式中的负号说明惯性质量块产生的惯性力与加速度方向相反。由式(4－36)求Fx
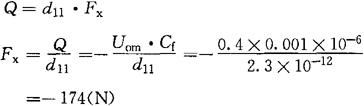
式中负号说明Fx是惯性质量块惯性力的反作用力。
6．弹性敏感元件的特性参数计算
(1)弹性圆柱(实心和空心)
柱式弹性元件结构简单，可承受很大的载荷，根据截面形状可分为实心和空心两种，如图4－28所示。
(a)实心圆柱
(b)空心圆柱
图4－28 弹性圆柱
在力的作用下，柱式弹性元件往往以应变作为输出量。在轴向承受作用力F(拉或压)时，与轴线成α角的截面上所产生的应力、应变为：
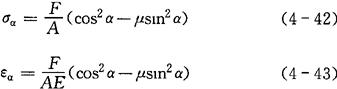
式中 F——沿轴线方向上的作用力(N)；
E——材料的弹性模量(N／m2)；
μ——材料的泊松比；
A——圆柱的横截面积(m2)；
α——截面与轴线的夹角(°或rad)；
σα——应力(N／m2)；
εα——应变。
在轴向(α=0°)产生的应力，应变为：
在横向(α=90°)产生的应力，应变为：
令
β=cos2α－μsin2α (4－48)
式中 β——灵敏度结构系数。
因而弹性圆柱应变的一般表达式为：
由上式得知，弹性圆柱的应变大小取决于弹性圆柱的灵敏度结构系数、横截面积、材料性质和弹性圆柱所承受的力，而与弹性圆柱的长度无关。
柱式弹性敏感元件主要用于电阻应变式传感器中。各种BLR型传感器的弹性敏感元件即为空心圆柱体。
(2)悬臂梁
悬臂梁是一端固定一端自由的弹性敏感元件。根据梁的截面形状不同可分为等截面梁和等强度梁(变截面)。
①等截面梁。图4－29为等截面悬臂梁。作用力F与梁上某一位置处的应变关系的计算为：
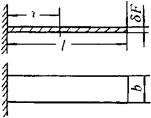
图4－29 等截面悬臂梁
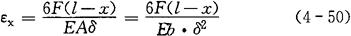
式中 εx——距定端为x处的应变值；
F——作用力(N)；
l——梁的长度(m)；
δ——梁的厚度(m)；
A——梁的截面积(m2)；
x——某一位置到固定端的距离(m)；
E——弹性模量(N／m)；
b——梁的宽度(m)。
β=6(l－x) (4－51)
式中 β——灵敏度结构系数。
②等强度梁。图4－30为等强度悬臂梁。等截面悬臂梁在不同部位所产生的应变是不相等的，而等强度悬臂梁在自由端加上作用力时，在梁上各处产生的应变值相等。为了保证等应变性，作用力F必须加在梁的两斜边的交汇点T处。等强度梁各点的应变值ε及灵敏度结构系数β为：
图4－30 等强度梁
β=6 (4－53)
7．电阻应变式传感器
电阻应变式传感器由弹性敏感元件与电阻应变片组成。弹性敏感元件在感受被测量时发生变形，其表面产生应变。粘贴在弹性敏感元件表面的电阻应变片也跟着产生变形，其阻值发生相应的变化。通过测量电阻应变片的阻值变化，就可以确定被测量的大小。
(1)应变片的结构
图4－31为电阻丝应变片结构示意图。电阻应变片是用直径约为0．025mm的具有高电阻率的电丝制成的。为了获得很高的电阻值，电阻丝排列成栅网状，并粘贴在绝缘基片上线栅上面粘有保护层，电阻丝两端焊有引出线。应变片规格一般以使用面积或电阻值来表示。如3×10mm2或120Ω。
图4－31 电阻丝应变片结构示意图
1－引出线 2－覆盖层 3－基底 4－电阻丝
(2)应变片的工作原理
电阻应变片的工作原理基于金属的应变效应。金属丝的电阻随着它所受的机械变形的大小而发生相应变化的现象称为金属的电阻应变效应。
实验证明，电阻应变片的电阻相对变化△R／R与应变ε的关系在很大范围内是线性的，即：
式中 △R——电阻应变片电阻的绝对变化(Ω)；
R——电阻应变片电阻(Ω)；
K——电阻应变片灵敏度系数；
ε——电阻应变片的应变，轴向应变以εx表示，横向应变以εy表示，εx与εy两者之间的关系为εy=－μεx。
(3)转换电路
常规应变片的电阻变化范围很小，而转换电路能精确地将电阻的变化转换成电压或电流输出。电阻应变片传感器中常用的转换电路是电桥电路。如图4－32所示。
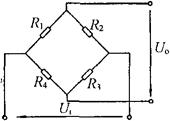
图4－32 桥式转换电路
根据不同的要求，桥式转换电路有以下几种工作方式：
①半桥、单臂工作方式。桥路中，R1为应变片，其余各臂为固定电阻，输出电压Uo与输入电压U1的关系为：
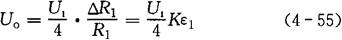
②半桥、双臂工作方式。桥路中，R1、R2为应变片，R3、R4为固定电阻，输出电压Uo与输入电压U1的关系为：
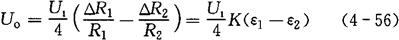
③全桥、四臂工作方式。桥路中，4个桥臂都为应变片，输出电压Uo与输入电压U1的关系为：
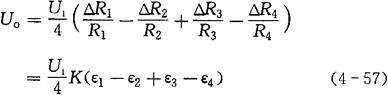
上两式中，各桥臂应变片的灵敏度K都相同。
［例4－15］ 有一个测量起重机起吊物重量的拉力传感器，如图4－33(a)所示。传感器中R1、R2、R3、R4贴在等截面轴上。已知等截面轴的截面积为0．00196m2，弹性模量E为2．0×1011N／m2，泊松比μ为0．30。R1、R2、R3、R4的标称阻值均为120Ω，应变片的灵敏度K为2．0，它们组成全桥转换电路，如图4－33(b)所示，桥路电源电压U1为2V，测得输出电压Uo为2．6mV。求：等截面轴的轴向应变及横向应变；重物m的质量。
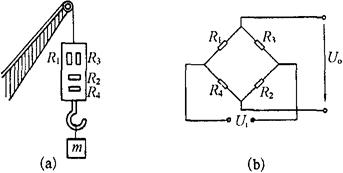
图4－33 测量吊车起吊重物重量的拉力传感器示意图
［解］ 等截面轴的轴向应变
由式(4－57)来求
由图4－32(a)得知，R1、R3感受的是轴向应变，即ε1=ε3=εx；R2、R4感受的是横向应变，即ε2=ε4=εy，而εy=－μεx。将这些关系代入上式可得
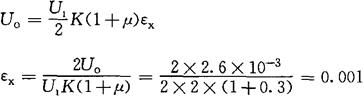
等截面轴的横向应变
εy=－μεx=－0．3×0．001=－0．0003
重物m的质量
由式(4－45)及式(4－57)来求
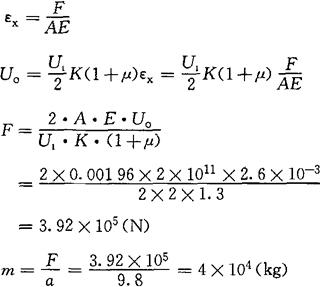
8．电容式传感器
电容式传感器是以各类型的电容器作为传感元件，通过电容传感元件将被测物理量的变化转化为电容量的变化，再经转换电路转换为电压、电流或频率。
电容式传感器广泛地用于位移、振动、角度、加速度、压力、液面、成分含量等方面的测量。
图4－34为平板电容器示意图。当忽略边缘效应时，平板电容器的电容量为：
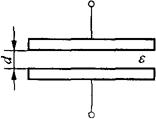
图4－34 平板电容器
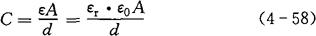
式中 C——电容(F)；
A——极板面积(m2)；
d——极板间间距(m)；
εr——相对介电常数；
ε0——真空介电常数，ε0=8．85×10－12Fm－1
ε——电容器极板间介质的介电常数。
由上式得知，在A、d、ε三个变量中，改变其中任何一项，均可使电容器的电容量C改变。由此可得三种类型的电容式传感器。
(1)变面积式电容传感器
变面积式电容传感器可分为直线位移和角位移等形式。
①直线位移式电容传感器。图4－35(a)为直线位移式电容传感器。设两极板遮盖面积为A，当动极板随被测物体移动x距离后，面积A发生变化，电容量C也随之改变，其关系为
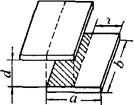
(a)直线位移型
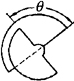
(b)角位移型
图4－35 变面积式电容传感器
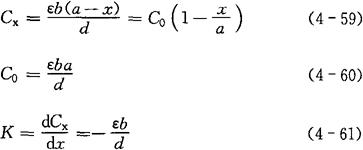
式中 ε——两极板间介质的介电常数；
a——极板宽度(m)；
b——极板长度(m)；
d——两极板极距(m)；
x——位移量(m)；
Cx——被测电容(F)；
C0——初始电容(F)；
K——灵敏度。
由灵敏度计算式得知，增大极板长度b，减小极距d，可提高直线位移式电容传感器的灵敏度。
②角位移式电容传感器。图4－35(b)为角位移式电容传感器。电容器的动片随被测物体转动θ角度时，两极板遮盖面积A发生变化，电容量C也随之改变，其关系为：
当θ=0时
当θ≠0时
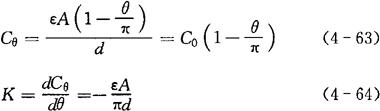
式中 Cθ——被测电容(F)；
θ——位移角(°或rad)。
由式(4－60)和(4－63)得知，灵敏度为常数，故变面积式电容传感输出性是线性的。变面积式电容传感器多用于位移检测。
(2)变极距式电容传感器
图4－36为变极距式电容传感器。当电容器极板间介质的介电常数ε和极板面积A不变，只改变两极板间的极距d时，则电容器的电容量C随之改变。
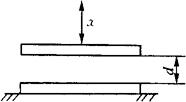
图4－36 变极距式电容传感元件原理图
设电容器的ε和A不变，初始状极距为d0时，其初始容量
C0为：
式中 C0——电容器的初始电容量(F)；
d0——电容器的初始极距(m)；
A——极板面积(m2)；
ε——两极板间介质的介电常数。
当电容器的动极板随被测物的作用而位移，使极板间的极距减小x距离时，其电容值为：
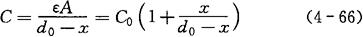
式中 C——电容(F)；
x——位移量(m)。
由上式得知，电容C与位移x之间不是线性关系。其灵敏度不是常数。
当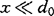
时，上式为：
此时C与x呈线性关系，但量程缩小很多。变极距式电容传感器的灵敏度为：
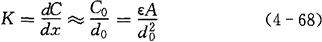
式中 K——灵敏度。
一般电容式传感器初始电容在20～300PF，极板距离在25～200μm的范围内，最大位移应该小于两极板间距的1／10。
在实际应用中，为了提高传感器的灵敏度，减小非线性，常把传感器做成差动形式，如图4－37所示，其电容值
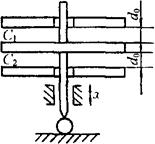
图4－37 差动式电容传感器结构示意图
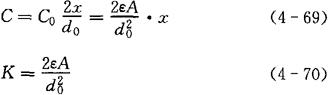
由上式得知，差动式变极距电容传感器的灵敏度比变极距式电容传感器的灵敏度提高一倍。
(3)变介电常数式电容传感器
①液位式。图4－38所示为电容液位计原理图。当被测液体的液面在电容式传感元件的内、外两同心圆柱形电极间变化时，引起极间不同介电常数介质的高度发生变化，因而导致电容变化，其电容量与液面高度的关系为
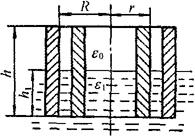
图4－38 同轴双金属管式电容液位计
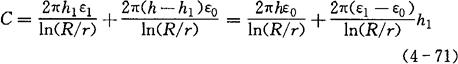
式中 h——电容器极板高度；
r——内圆柱形电极的外半径；
R——外圆柱形电极的内半径；
h1——液面高度；
ε1——被测液体的介电常数；
ε0——真空的介电常数。
由式4－71可见，输出电容C与液面高度h1呈线性关系。其灵敏度为
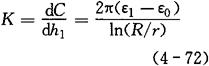
②测厚式。图4－39为测厚式变介电常数电容传感器。当某种介质处于两固定极板间时，电容量与介质参数之间的关系为：
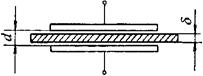
图4－39 变介电常数的电容式传感器
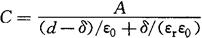
式中 δ——运动介质的厚度；
εr——介质的相对介电常数，εr=ε1／ε0。
由式4－73可见，当介质的厚度δ保持不变而介电常数εr改变，如湿度变化，电容将产生相应的变化，因此可作为介电常数ε测试传感器，如湿度传感器。反之，若εr不变，则可作为测厚传感器。
(4)电容式传感器的转换电路
电容式传感器将被测物理量转换为电容变化后，常采用差动桥式转换电路将其转换为电压、电流等信号。
图4－40为电容传感器差动桥式转换电路。其输出电压为：
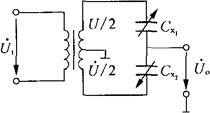
图4－40 电容传感器差动桥式转换电路
式中 Uo——转换电路输出电压(V)；
U——变压器次级电压(V)；
△C——传感器电容的变化值(F)；
C0——传感器的初始电容值(F)。
［例4－16］ 用一个角位移变面积式电容传感器测量一位移，传感器电容初始值C0=0．3μF，动片转动的位移角θ=30°，传感器接入差动桥式转换电路，变压器次级电压U=24V。求传感器的电容Cθ，电容变化值△C及转换电路的输出电压。
［解］ 传感器的电容值及电容变化值
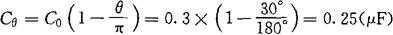
△C=Cθ－C0=0．25－0．3=－0．05(μF)
转换电路的输出电压
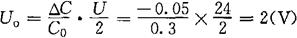
9．光栅位移传感器
(1)莫尔条纹
由大量等宽等间距的平行狭缝组成的光学器件称为光栅，如图4－41所示。透射光栅是在透明玻璃上刻出大量等宽间距的平行刻痕，每条刻痕处是不透光的，而两刻痕之间是透光的。光栅的刻痕密度一般为每mm10、25、50、100线。刻痕之间的距离为栅距W。如果把两块栅距W相等的光栅面平行安装，且让它们之间有较小夹角
时，则光栅上会出现若干明暗相间的条纹，即莫尔条纹，如图4－42所示。莫尔条纹是光栅非重合部分光线透过而形成的亮带，如图4－42中d－d线区所示。f－f线区则是由光栅的遮光效应形成的。
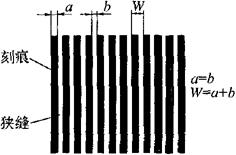
图4－41 光栅结构放大图
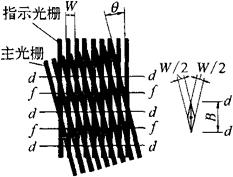
图4－42 莫尔条纹
莫尔条纹的特性：
①当指示光栅不动，主光栅左右平移时，莫尔条纹将沿指示栅线的方向上下移动。
②莫尔条纹有位移放大作用。当主光栅沿刻线垂直方向移动一个栅距W时，莫尔条纹移动一个条纹间距B。当栅间夹角θ较小时，主光栅移动一个栅距W，莫尔条纹则移动KW距离，K为莫尔条纹的放大系数，其运算关系为：
K=B／W≈1／θ (4－75)
式中 K——莫尔条纹的放大系数；
B——莫尔条纹间距；
W——光栅的栅距；
θ——栅间夹角。
莫尔条纹间距与光栅栅距的关系为：
B=W／θ
由以上算式得知，当θ角较小时，例如θ=30′，则K=115，表明莫尔条纹的放大倍数很大。这样可把肉眼看不见的光栅位移变为清晰可见的莫尔条纹移动，从而可实现高灵敏度的位移测量。
(2)光栅位移传感器
光栅位移传感器由主光栅、指示光栅、光源和光电器件组成，如图4－43所示。主光栅随被测物体而位移，莫尔条纹也跟着产生移动，通过光电器件的信号转换并记数，从而反映了被测物体的位移量。
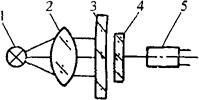
图4－43 黑白透射光栅传感器光路
1－光源 2－聚光镜 3－主光栅 4－指示光栅 5－光电元件