一些基本概念、常用的公式和计算方法
出处:按学科分类—工业技术 企业管理出版社《计量专业工程师手册》第291页(17689字)
1.有源元件
在有源元件中进行着化学能、机械能或其它形式的能量转变成电能的过程。如线路中常用的各种电源属有源元件。
(1)电动势源:是具有两个端钮的有源元件,它两端的电压u(t)不随其中所流过的电流而变。这是理想元件。实际电能源的电路图可表现为电动势源与表征它的内电阻和电感的无源元件相串联的形式,称为电压源。
(2)电流源:是一种有源元件,它的电流i(t)不随端电压而变。这也是理想元件,在一些情况下,为了简化计算可应用这概念。
2.无源元件
与有源元件相对应的元件,即其内部没有其它能量转换为电能的元件。如电阻、电感、电容等是无源元件。对这类元件,可分为定常(特性曲线不随时间变化)、时变(特性曲线随时间变化)、线性(元件中的电压和电流彼此用一次线性方程一代数方程或微分方程一相联系)和非线性四种。下面主要对线性定常元件的特性进行分析介绍。
(1)电阻器:电阻r是这样的元件,当有电流流过它时,在其中将发生电能转变成热能的不可逆过程。其值等于它两端的电压ur与通过其中的电流i之比:r=ur/i。
(2)电感器:电感L是能够储藏磁场能量的电路元件。同时它也表示等于自感磁链ψ(=NΦ,如所考虑的元件是一个具有N匝的线圈,并假定通过每一圈的磁通量都是Φ)与电流i之比的磁量:L=ψ/i。
自感电动势等于磁链的变化率,即eL=-dψ/dt=-L·di/dt。
电感上的电压为:uL=-eL=L·di/dt。
(3)电容器:电容C是能够储藏电场能量的元件,同时它亦表示等于这元件上的电荷q与电压uC之比的电气量:C=q/uC。
当电容器上的电压变化时,在电路中出现电流,其数值由电荷变化的速率确定
i=dq/dt或i=C·duc/dt。
(4)互感:如果与一个电感元件相交连的磁链,其中的一部分同时与另一个电感元件相交链,则这两个电感元件除了具有参数L1和L2之外,还具有被称为互感的参数M。当磁通和与之相应的磁链是电流的线性函数时,这个参数以互感磁链与电流之比来确定:
M=ψ12/i2和M=ψ21/i1
式中ψ12是由第二元件内的电流所产生的第一元件的磁链;ψ21是第一元件内的电流所产生的第二元件的磁链。在这种情况下,在第一元件和第二元件中将感应互感电动势,其值等于:

3.线性电路
由线性有源元件及无源元件组成的电路。
实际的电气装置严格说来很难完全服从线性规律,如在具有铁芯的电感线圈中当电流变化时,磁通和电流之间的比值并不保持常数,电流通过电阻时电能转变成热能,电阻温度发生变化,使其阻值也随之发生变化,根据电介质的类型,在一定程度上电容也能变化,且电容器的电容是外加电压的函数。在大多数情况下非线性都比较小,可以忽略,但在计量工作中,特别是测量准确度要求很高时.就必须考虑非线性的影响。
4.能量和功率
在某一外加电压作用下,电流通过电路中某一元件在一定时间间隔内所作的单元功(或在同一时间内进入该元件的单元能量)等于dW=udq=uidt。在国际单位制中能量的单位为焦耳(J)。
p=dW/dt=ui (6.2-15)
即等于电压与电流瞬时值的乘积。功率是一代数量;如电压和电流的正方向选择得相同,则当p>0时,能量由电源进入受电器,而当p<0时,能量由所研究的电路返回电源。
电路中不同元件的功率和能量的瞬时值表达式:
(1)电阻所消耗的功率和能量分别为

(2)电感两端的功率及其磁场能量为

(3)电容两端的功率及其电场能量为

5.周期电气量的有效值和平均值
周期性变化的电压或电流的数值,通常按一周期内的有效(均方根)值来判断。所谓周期电流和电压的有效值是指数值

周期电流和电压的平均值为

6.正弦电流和电压的有效值、平均值与其最大值的关系

式中,I、 、Im分别为正弦电流的有效值、平均值和最大值;
、Im分别为正弦电流的有效值、平均值和最大值;
U、 、Um分别为正弦电压的有效值、平均值和最大值。
、Um分别为正弦电压的有效值、平均值和最大值。
7.正弦函数的表示法
以正弦电压u=Umsin(ωt+φ)为例,u表示瞬时值,Um表示最大值,ωt为幅角,ω称为角频率,它与周期和频率之间的关系为ωT=2π或ω=2πf,φ称为初相角,可随坐标原点的选择而变。量ω具有1/秒的因次,以弧度/秒计算,初相角φ与ωt的单位相同,为弧度。当角φ以度来计算时,幅角ωt也应化成度。
8.具有相同角频率的正弦电量之间的相位关系
设两个具有相同角频率的正弦电量为
u1=U1msin(ωt+φ1),u2=U2msin(ωt+φ2)
则初相之差φ=φ1-φ2称为这两正弦电量的相位差或u1对u2相位差角。当相位差角φ=0时,两正弦量称为同相,φ=180°时,称为反相。当φ1>φ2即φ>0时,称量u1相位超前于u2,或u2相位滞后于u1。
9.在R、L、C元件中正弦电压与电流之间的关系,感抗、感纳、容抗、容纳、电抗、电纳
(1)电阻R两端的电压uR和通过该电阻的电流iR是同相的;
(2)当正弦电流iL(=Imsin(ωt+φ))流过电感时,电感上的电压UL越前于电流的角度为π/2,如下式所示

式(6.2-27)表明,Um=ωLIm,用有效值表示时,U=ωLI。
量值XL=ωL具有电阻的因次,称为感抗。其倒数YL=1/ωL称为感纳。
(3)如电容上的电压是正弦的,即uC=Umsin(ωt+φ),则流过电容的电流iC越前于电压uC的角度为π/2。如下式所示:

式(6.2-28)表明,Um=(1/ωC)Im,用有效值表示时,U=(1/ωC)I。
量值XC=1/ωC具有电阻的因次,称为容抗。其倒数YC=ωC称为容纳。
(4)当一感抗和容抗串联时, ,称为电抗。
,称为电抗。
(5)当一感纳和容纳并联时, ,称为电纳。
,称为电纳。
10.R、L、C串联电路的总阻抗及阻抗角
如图6.2-1所示的R、L、C串联电路的总阻抗(阻抗模)Z及流过该电路的电流与电路两端的电压的相位差φ分别为:

图6.2-1 R、L、C串联电路

φ又称为这串联阻抗电路的阻抗角。
11.R、L、C并联电路的总导纳及导纳角
如图6.2-2所示的R、L、C并联电路的总导纳(导纳模)Y及流过该电路的总电流与电路两端的电压的相位差φ分别为:


图6.2-2 R、L、C并联电路

φ又称为这并联阻抗电路的导纳角。
12.电压谐振和电流谐振
当R、L、C串联电路的感抗等于容抗,即X=XL-XC=0时,电流与电压同相.电路的这种工作状态,称为电压谐振。
而当R、L、C并联电路的感纳等于容纳,即B=BL-BC=0时,电流与电压同相.电路的这种工作状态,称为电流谐振。
在上述电压谐振或电流谐振的情况下,谐振频率均为:

13.品质因数、损耗因数、损耗角
品质因数Q:对于无辐射系统,如果Z=R+jX,则Q=|X |/R。对于以R、L串联电路表示的电感线圈,其品质因数QL=ωL/R,并与线圈阻抗角的正切等值。对于以R、C并联电路表示的电容器,其品质因数QC=ωCR,QC的倒数与电容器导纳角的正切等值。
损耗因数d=1/Q,即等于品质因数的倒数。
损耗角δ=arctgd。
在电工技术中,常用品质因数来评价电感线圈,用损耗因数来评价电容器。
对于上述电压、电流谐振电路,在谐振频率下电路的品质因数为:
电压谐振时, ;电流谐振时,
;电流谐振时, 。
。
14.给定电路中阻抗和导纳的变换
如给定电路的电导为G,电纳为B,则变换为用电阻和电抗表示时,

如给定电路的电阻为R,电抗为X,则变换为用电导和电纳表示时,

15.交流电量的复数表示法
(1)有关复数的基本知识
如图6.2-3的复平面上(横坐标为实轴,纵坐标为虚轴)的一点a表示着复数
A=A1+jA2 (6.2-36)

图6.2-3 在复平面上复数的几何表示法
式中 ,上式是复数的代数形式写法。
,上式是复数的代数形式写法。
复数的极坐标形式为:
 (6.2-37)
(6.2-37)
复数的指数形式则为:
 (6.2-38)
(6.2-38)
式(6.2-37)和(6.2-38)中A为复数的模,α为复数的幅角或相位。因为A1=Acosα,A2=Asinα,则

α=arctgA2/A1 (6.2-39b)
复数的三角形式写法为:
 (6.2-40)
(6.2-40)
复数的相等:两复数的实部和虚部分别相等,则认为该两复数相等。
共轭复数:如果两复数的模相等,其幅角也相等但符号相反,则称该两复数互为共轭。两共轭复数可如下式表示:


共轭复数的一个重要性质:两个互为共轭的复数之积为实数,且等于其因子模的平方,即
 (6.2-41)
(6.2-41)
复数的运算方法可参考有关资料。
(2)正弦函数的复数表示法
正弦函数可用一旋转矢量来表示,而终端以角速度沿正方向(反时针方向)旋转的矢量,在复平面上又可表示为
 (6.2-42)
(6.2-42)
式中 是表示给定矢量在t=0瞬间的复振幅。因子ejωt是旋转因子,一复数乘以ejωt就表示矢量
是表示给定矢量在t=0瞬间的复振幅。因子ejωt是旋转因子,一复数乘以ejωt就表示矢量 沿正方向旋转ωt角度。
沿正方向旋转ωt角度。
式(6.2-42)可表示为三角形式:
Aej(ωt+α)=Acos(ωt+α)+jAsin(ωt+α) (6.2-43)
即任何正弦函数Asin(ωt+α)可视为不带因子j的复函数的虚部。在数学上可以下式来记述: (6.2-44)
(6.2-44)
符号Im(Imaginare)表示只取复函数的虚部,但去掉因子j。
同样,余弦函数可用复函数的实部来表示:
 (6.2-45)
(6.2-45)
式中符号Re(Real)表示只取复函数的实部。
正弦函数的加、减、微分及积分运算可用对复函数虚部进行相同的运算来代替,而对复函数虚部的运算又可用对复函数本身的运算来代替,然后取其所得结果的虚部。必须注意,这一法则不能推广到乘除运算上。
(3)正弦电量的复数表示法
如图6.2-1的R、L、C串联电路两端的电压为u=Umsin(ωt+ψ),电流为i=Imsin(ωt+ψ-φ),用复数表示时可分别写为 和
和 。相应地,电压和电流的复振幅分别为
。相应地,电压和电流的复振幅分别为 和
和 。
。
对于图6.2-1的电路,其总阻抗用复数表示时为

对于图6.2-2的电路,其总导纳用复数表示时为

16.正弦电流电路中的功率
(1)瞬时功率:当u=Umsinωt,i=Imsin(ωt-φ)时,瞬时功率为:
p=2UIsinωtsin(ωt-φ)=UI[cosφ-cos(2ωt-φ)] (6.2-48)
上式表明,瞬时功率由两部分组成,恒定量UIcosφ和正弦量UIcos(2ωt-φ)。
(2)有功功率:在一周期内的平均功率,称为有功功率,它等于式(6.2-48)的恒定分量。

有功功率以瓦特(W)计量。因子cosφ称为功率因数。
(3)视在功率:又称表观功率,用符号S或Ps表示,S=UI,即为电压与电流的有效值的乘积,视在功率的单位为伏安(VA)。由P及S的表达式可得,功率因数等于有功功率与视在功率之比:cosφ=P/S。
(4)无功功率:用符号Q或PQ表示,

无功功率的单位也是伏安(V·A),过去电工技术中常采用IEC规定的乏(var)作为无功功率的单位名称和符号,但国际计量大会没有采用它为SI单位。
(5)复功率:用复数量 表示复数形式的功率,称为复功率。由下式可见,复功率的实部等于有功功率,虚部等于无功功率,复功率的模S等于视在功率。
表示复数形式的功率,称为复功率。由下式可见,复功率的实部等于有功功率,虚部等于无功功率,复功率的模S等于视在功率。
 (6.2-51)
(6.2-51)
17.电源向受电器传输最大功率的条件
当电压源的阻抗用Z0=R0+jX0表示,负载阻抗用Z=R+jX表示时,电源向受电器传输最大有功功率的条件为
 0 (6.2-52)
0 (6.2-52)
而输出最大视在功率的条件为负载的阻抗等于电源的阻抗,即Z=Z0。
18.线性电路连接图的变换
(1)星形变换为等效的多角形:
当n-多角形支路的复阻抗满足条件

时,图6.2-4中的n-射线星形和n-多角形电路是等效的。

图6.2-4 n-射线星形变换为n-多角形
式(6.2-54)表明,多角形的边和对角线的导纳等于连接在相同端钮上星形射线导纳之积除以所有射线导纳的总和。
三射线星性变换为与其等效的三角性的阻抗公式:
Z12=Z1Z2/Z,Z23=Z2Z3/Z,Z31=Z3Z1/Z, (6.2-55)
式中 

(2)三角形变换为等效的三射线星形变换公式为:


图6.2-5 三射线星形变换为三角形以及相反的变换
即:射线阻抗等于三角形邻边的阻抗之积除以三边阻抗的总和。
(3)等效电压源和等效电流源
两种不同的电源——电压源和电流源,如用一种电源代替另一种电源,与这些电源相联接的外部电路中的电压和电流保持不变时,称这两种电源等效。
如图6.2-6a和b所示的电压源和电流源,它们的电动势 和电流
和电流 之间满足下式的关系时,两电源等效。该式称为等效电压源和电流源的法则。
之间满足下式的关系时,两电源等效。该式称为等效电压源和电流源的法则。

图6.2-6 等效的电压源和电流源
 (6.2-58)
(6.2-58)
19.回路电流法:
回路电流法是在电路中全部阻抗和电动势已知时,根据基尔霍夫第二定律求解电路各回路中的环行电流的方法。
设已知电路包含n个独立回路,按基尔霍夫定律可列出含n个方程的方程组:

式中Ui是回路i中的回路电动势,即在该回路中作用的电动势的代数和,方向与回路循行方向相同的电动势取正号,方向与回路循行方向相反的电动势取负号。
Zii是回路i的自阻抗(即只属于i回路的复阻抗的和);
Zik是回路i与回路k的共阻抗(即同属两个回路的复阻抗)。
当回路的循行方向与所选的电流Ii的正方向相同时,自阻抗Zii取正号,当回路的循行方向与所选的电流Ik的正方向相反时,共阻抗Zik取负号。
应用行列式解方程组便可求得各回路电流:

方程组(6.2-60)可简写为:

式中

△ik是行列式(6.2-62)中元素Zik的代数余因式,第一个下标(i)表示行列式中划去的行的号码,也表示与这个代数余因式相乘的回路电动势所在的回路的号码;第二个下标(k)表示行列式中划去的列的号码,对应于要求其回路电流的回路的号码。
20.节点电压法
节点电压法就是在已知电路中的电流源及各支路导纳时按基尔霍夫第一定律决定各个节点对于某个参考节点的电压的方法。对于有q个节点的回路可列出q-1个方程:


式中,流入节点的电流取正号,流出节点的电流取负号;Ya是接到节点i的全部支路的自导纳;Yik是节点i和k间的共导纳,只要选取节点电压的正方向是指向参考节点,共导纳总带有负号。
应用行列式解方程组(6.2-63),得到节点k对于参考节点的电压的公式:

式中

而△ik是该行列式中元素Yik的代数余因式,其第一下标(i)表示行列式中划去的行号,也表示其给定电流与这个代数余因式相乘的节点的号码;第二下标(k)表示行列式中划去的列号,对应于要求其节点电压的节点的号码。
21.叠加法
式(6.2-61)和(6.2-64)表明,线性电路中任何回路的电流可以由各电动势单独作用时在该回路中所引起的电流代数相加求得;而任何节点的节点电压可以由各电流源单独作用时在该节点所引起的电压代数相加求得。根据这一原理,通过求各电动势轮流作用时在同一回路(或支路)中所产生的电流,然后把所得电流代数相加以求得所要计算的回路电流的方法,称为叠加法。
22.入端阻抗、入端导纳和互阻抗、互导纳
如图6.2-7a中所示,已知电路的回路i和k,及无源网络Ⅱ,则电动势 与在回路i中产生的电流
与在回路i中产生的电流 的比值称为电路的入端阻抗:
的比值称为电路的入端阻抗:


图6.2-7 入端阻抗、互阻抗和入端导纳、互导纳的定义说明图
电动势 与在回路k中产生的电流
与在回路k中产生的电流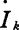 的比值称为回路i与k的互阻抗(转移阻抗):
的比值称为回路i与k的互阻抗(转移阻抗):

如图6.2-7b所示,假定把电流源接到电路的节点i上,而电路的其余部分都是无源的,按(6.2-64)式可求得节点i和k上的电压 和
和 ,则电流
,则电流 与节点电压
与节点电压 的比值称为电路的入端导纳:
的比值称为电路的入端导纳:

而电流 与节点电压
与节点电压 的比值称为节点i和k的互导纳(转移导纳):
的比值称为节点i和k的互导纳(转移导纳):

23.互易定理
含电动势源的情况。如果位于电路任一回路中的某个电动势在该电路的另一回路中产生电流,则移入第二回路的同一电动势将在第一回路中产生同样大小的电流。
含电流源的情况。如果已知电路中任一节点的电流源在任意两节点间产生某一电压,则把同一电流源接于上述两节点间时必将在第一个节点出现数值相同的电压。
24.补偿定理
如果把电路的任一回路中的阻抗用大小等于该阻抗上的压降而与流经该阻抗的电流方向相反的电动势来代替时,电路中的电流不变。
25.关于支路阻抗变化时电路中电流变化的定理
如果电路的任一支路阻抗数值变化±Z′,则电路中电流的变化,将与作用在变化支路中方向与该支路中原来的电流方向相反、而数值和符号与±Z′I相同的电动势所引起的变化相同。
26.等效电源定理(戴维南定理)
等效电压源定理:在线性电路中,与任何一条支路mn相连接的电路,如用等效电压源代替,该支路中的电流不会改变。这个电源的电动势应该等于断开支路mn的端电压,而电原的内阻抗应该等于mn支路断开时端钮m与n间的无源网络的阻抗。
等效电流源定理:在线性电路中,如用等效电流源代替与任何一条支路mn相连接的电络,则mn支路中的电流不会改变。这个电源的电流应该等于把端钮m与n短接后流过mn支路的电流,而电源的内导纳应该等于mn支路断开时端钮m与n间的无源网络的导纳。
27.互感电路计算的特点
引起互感电动势的电路称为感应耦合电路。感应耦合元件的所谓同向联接*:同向联接时每个元件中的自感磁通和互感磁通的正方向相同。一般用星号*来标记同名端或同极生,如图6.2-8所示。

图6.2-8 感应耦合元件(同向联接)
感应耦合元件的同名端表示下述特性:当电流i1和i2对这些端钮的方向相同时,在每个元件中的自感磁通与互感磁通相互加强;向一个元件的同名端引入数值增大的电流,将会在另一个元件的同名端引起电位的升高。
如图6.2-9a所示含同向联接线圈的电路同具有电阻R′=R1+R2及电感L′=L1+L2+2M的一个线圈是等效的。

(a)同向联接;(b)反向联接
图6.2-9 感应耦合元件的串联
而如图6.2-9b所示含反向联接线圈的电路同具有电阻R′=R1+R2及电感L′=L1+L2-2M的一个线圈是等效的。
按式(6.2-14),在同向联接时互感电动势的复数表示式为 ,从而互感电动势和互感电压降的复有效值分别为:
,从而互感电动势和互感电压降的复有效值分别为:
 , (6.2-70)
, (6.2-70)
式中jωM是复互感抗。在同向联接时互感电压降的表达式取正号,反向联接时则取负号(假设在两种情况下电路的循行方向都与电流的正方向一致)。
28.耦合系数
表征两个电路元件感应耦合程度的系数,为

式中L1和L2是电路元件的电感,M是互感。耦合系数恒小于1,因为在一个元件中的电流不可能与第二个元件的各匝完全交链,而有漏磁现象存在,其大小可以用漏感Ls来表示:

式中n=ω1/ω2,为第一个元件和第二个元件的匝数比。
29.空心变压器的方程及代换电路
图6.2-10的空心变压器,当电压和电流为正弦时,其变压器方程为:
 (6.2-73)
(6.2-73)

或  (6.2-74)
(6.2-74)

后一对方程是对应于图6.2-11所示电路的回路方程。该电路可看成是空芯变压器的代换电路。图中差值L1-M和L2-M只在原、副绕组匝数相同(ω1=ω2)时才有意义。ω1≠ω2时,实际上常采用图6.2-12所示的折合到原边的电路来代换。折合是把电压 和电流
和电流 化为原边绕组的数值来代替:电压
化为原边绕组的数值来代替:电压 乘n,电流
乘n,电流 除以n,n=ω1/ω2。变压器折合后的代换电路的回路方程为:
除以n,n=ω1/ω2。变压器折合后的代换电路的回路方程为:

图6.2-10 空芯变压器

图6.2-11 空芯变压器的代换电路

由上式可见,代换电路中包含了变压器原边绕组的电阻r1及漏感Ls1、横支路(磁化支路)中的电感(ω1/ω2)M、折合到原边的并乘以匝比平方的副边绕组的电阻r2及漏感Ls2。流经磁化支路的电流 称为变压器的磁化电流。
称为变压器的磁化电流。
由于副边绕组的电压和电流折合到原边后数值同匝比成比例地变化,因此该电路与变压器的原始电路并不等效。为使代换电路成为给定变压器的等效电路,可将一个在任何条件下原电压与副电压之比恒等于副电流与原电流之比、且没有能量损失的理想变压器接在图6.2-12的输出端,如图6.2-13所示。

图6.2-12 折合到原边绕组的代换电路

图6.2-13 n=w1/w2时空芯变压器的等效电路
30.变压器的入端阻抗
如图6.2-14a所示,当负载ZH经变压器与电源联接时,变压器的入端阻抗可通过变压器回路方程求得:

图6.2-14 决定变压器入端阻抗的等效电路

式中第三项是从副电路引入原电路的复阻抗;在理想变压器的情况下,M2=L1L2,r1=r2=0,式中L1和L2为无限大,则式(6.2-76)变为:
Z=n2·ZH (6.2-77)
这是因为当L1和L2趋近无限大时,它们的比值保持有限值,绕组的电感与匝数的平方成正比。由此可见,负载与电源之间联接的理想变压器按变比的平方的比例改变着负载阻抗。在实际中可利用来控制电源及负载的阻抗,以提高电源的输出功率。
31.有关三相交流电的基本知识
(1)三相对称正弦交流电各相电流频率相同而相互间相位相差2π/3。
(2)三相电的联接法:联接方法通常有两种,如图6.2-15所示。图中的两种接法都是星形联接,即发电机和负载的三个相都将末端接在一起,成为三射线星形,联接点称为中性点。图中a)的接法是三相四线制,即电源和负载的中性点联接起来,称为中线,而发电机的三相输出线称为火线。由于三相的电流相位上对称而负载一般也尽量安排得接近对称,因此中线上电流接近于零(完全对称时为零)。当把中线去掉时,则得图6.2-15b)所示的三相三线制接法。发电机也可接成三角形接法,即每一相的首端和另一相的末端相联接。发电机的三相接成三角形时,必须注意使三角形所形成的回路中的电势为零,这样才能保证在没有负载(即外端开路)的情形下发电机内部不致有循环电流。


图6.2-15 三相电的联接法-星形接法示意图 。
。
(3)线电流、相电流、线电压、相电压:端线(火线)上的电流称为线电流,每相内的电流称为相电流;引出线之间(即各相之间)的电压称为线电压,而每相的电压(即端点与中性点之间的电压)称为相电压。
在星形接法中(无论是三相三线制或三相四线制),相电流就是线电流;当正弦相电压为对称时,线电压在数值上为相电压的 倍,即
倍,即 ,而在相位上越前于先行相(例如对于AB间线电压而言,先行相即为A相)相电压30°。我国的供电系统在用户端处采用相电压为220V,则线电压为380V。
,而在相位上越前于先行相(例如对于AB间线电压而言,先行相即为A相)相电压30°。我国的供电系统在用户端处采用相电压为220V,则线电压为380V。
(4)三相正弦电路中的平均功率:等于各相电路中平均功率的和。在已知各相电压电流的有效值和功率因数时,可写为
P=UAIAcosφA+UBIBcosφB+UcIccosφc,
在相电压和相电流均对称时,
32.磁路计算
实际的磁路计算比较复杂,因非线性的因素较多,下面只介绍恒定磁通磁路的计算。
(1)恒定磁通无分支磁路的计算
计算的问题可分为两类,一为已知磁通求磁势,另一为已知磁势求磁通。
已知磁通求磁势的计算步骤(如图6.2-16a的无分支磁路)

图6.2-16 恒定磁通磁路计算示意图
1)按照材料及截面的不同进行分段;
2)作出中心线,按照所给尺寸计算出磁路各段的截面积S1、S2……和长度l1、l2……;
3)按已知的磁通计算各个段落的磁感应强度:

4)从各材料的B-H曲线(平均磁化曲线)上按已算出的磁感应强度B1、B2、……找出与它们相对应的磁场强度H1、H2、……;
5)按磁路的基尔霍夫第二定律求出所需要的磁势:
Iω=∑Hl=H1l1+H2l2+……。 (6.2-78)
当所给磁路中有空气隙时,则可应用真空中的磁导率μ0=4π×10-7H/m,由空气隙的磁感应强度B0计算其磁场强度H0:
H0=B0/μ0 (6.2-79)
实际上在空气隙的边沿处磁通向外部发散,造成所谓边沿效应,其作用等于增大了空气隙的面积,且空气隙越长此种作用越明显。从理论上计算空气隙的磁阻或磁导是很困难的,实际上常利用一些经验公式或已制好的曲线进行计算。但若空气隙的长度l0很小(例如较矩形铁梗的短边的20%为小),则认为空气隙的有效面积就等于铁梗的端面积也不会带来太大的误差。
已知磁势求磁通的计算:
考虑到磁路的非线性,必须应用如同计算非线性电路的方法,即应用猜试法或图解法。在应用猜试法时,如果磁路中含有不太短的空气隙,则因空气的导磁率比铁的导磁率小得多,以致其磁阻很大,大部分磁势的安匝数消耗在空气隙内。故第一次试猜时可认为全部磁势的安匝数都作用在空气隙,而磁通为Φ=μ0IωS0/l0,式中S0和l0分别为空气隙的截面积和长度。有了这个估计再进行图解法求解,就可获得较准确的结果。
(2)恒定磁通分支磁路的计算
工程上常遇到的是对称分支磁路,对这些对称分支磁路常可以分割开作为无分支磁路计算。如图6.2-16b的磁路就可从中央剖开成两半,而取其一半来计算,如图6.2.16c所示。剖分以后中间铁梗的截面积由S2变为S2/2,磁通由Φ2变为Φ2/2,但应注意磁势Iω仍不变。
对于非对称的分支磁路,则可根据给定的参数,利用磁路的基尔霍夫第一和第二定律,由已知量一步一步地推算出待求量,这里不再细述。
【参考文献】:
[1]国家技术监督局发布,GB3100~3102-93量和单位国家标准,中国标准出版社,1994年12月。
[2]王江主编,现代计量测试技术(第18章电磁计量技术),中国计量出版社,1990年12月。
[3]程守洙、江之永主编,普通物理学第二册,人民教育出版社,1979年2月。
[4]俞大光编,电工基础,人民教育出版社,1958年9月。
[5]Г.И.阿塔别柯夫,线性电路理论,人民教育出版社,1963年12月。
[6]C.A.狄苏尔、葛守仁,电路基本理论,人民教育出版社,1979年1月。
[7]乔蔚川、刘瑞珉、沈平子,The Absolute Measurement of the Ampere by Means of NMR,IEEE Trans.Instrum.Meas.,vol.IM-29,No.4,Dec.,1980.
[9]张钟华等,NIM用计算电容测定的量子化霍尔电阻的SI值(英文),计量学报,第16卷,第1期,1995年1月。
[10]刘瑞珉、刘恒基、金惕若等,NIM对γ′p及2e/h的SI值的最新测定结果(英文),计量学报,Vol.16,No.3,1995年7月。
[11]B.P.Kibble。I.A.Robinson and J.H.Belliss,A Realization of the SI Watt by the NPL MovingCoil Balance,CCE Documents 88-16,1988.
[12]P.T.Olsen。R.E.Elmquist,E.R.Williams,G.R.Jones and V.E.Bower,A Measurement of the NBS Electrical Watt in SI Units,CCE Documents 88-37,1988.
[13]Report of the 18th Meeting of CCE,1988.
[14]B.P.Kibble,I.A.Robinson and J.H.Belliss,The New NPL Moving Coil Balance-A Progress Report,CCE Documents 92-61,1992.
[15]唐统一、张钟华、张叔涵主编,近代电磁测量,中国计量出版社,1992年8月。
[16]袁楠、沈平子编,电磁量的单位制和单位的复现与传递,机械工业出版社,1986年4月。
[17]阮永顺、迈淑琴、王晓超编着,交流电桥检定与测试技术,中国计量出版社,1991年5月。
[18]唐佐梁、梁德正等,电能计量手册,河南科学技术出版社,1990年12月。
[19]K.J.Lentner.A Current Comparator System to Establish the Unite of Electrical Energy at 60 Hz,IEEE Trans.Instr.Meas.Vol.23,No.4,p.334-336,Dec.,1974.
[20]ю.B.阿法拉谢耶夫等着[苏],张伦译,磁场参数测量器具,科学出版社,1983。
[21]p.Φ.阿克纳叶夫、Л.И.留必莫夫、A.M.巴纳休克-米罗维齐着,李绍贵,王登安译,电磁量计量器具的检定,中国计量出版社,1992年5月。