轴的刚度计算

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册中》第1085页（1496字）

轴的刚度可分两大类：弯曲刚度和扭转刚度。对于轴的弯曲刚度，通常用挠度y及偏转角θ来度量。轴弯曲的允许变形量可参考表4．6-13。求阶梯轴的弯

曲变形，通常采用变形能量法。其步骤是：先绘制

如图4．6-7所示轴的外形图及弯矩图M(图b)，欲计算C处的挠度y_c，则在C处加一与变形方向相同的单位力，并绘出其弯矩图M′(图c)；欲计算A处的偏转角θ_A，则在A处加一与变形方向相同的单位力矩，并绘出其弯矩图M′(图d)。然后，按M、M′及截面的连续性，把轴分成为若干段。轴段的划分，以各阶梯的截面变化处和各作用力(实际载荷、单位力及支反力)的作用点作为轴段的分界点，如图a、b、c分为五段，图d分为四段。轴在欲计算截面处的挠度y或偏转角θ，可由下式求得：

式中 E为轴材料的弹性模量；I为截面惯性矩；M为轴上实际载荷产生的弯矩；M′为单位载荷(单位力或单位力矩)产生的弯矩；为第i段轴段的长度，各种轴段的积分值见表4．6-14。

图4．6-7 用变形能量法求轴的弯曲变形简图

表4．6-14 各种轴段的积分值

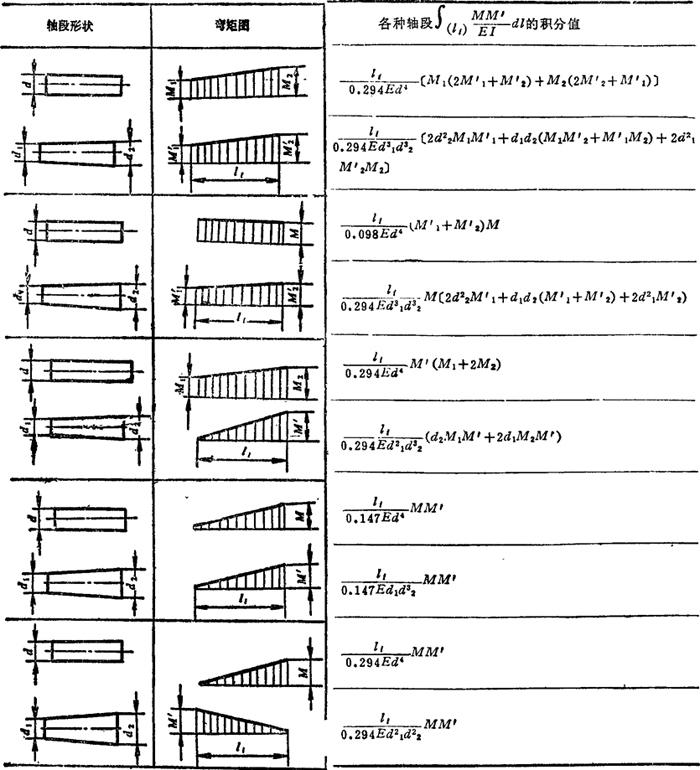
注：① 弯矩图中，其一选为实际载荷引起的，另一则作为单位载荷所引起的。

② 若M和M′方向相反，则其中之一取为“正”，另一为“负”。

③ 空心圆柱形轴段，用d⁴－d⁴₀代替表中d⁴(d₀为空心轴内径)。

轴的扭转角的计算式见表4．6-15，许用扭转角〔φ〕见表4．6-13。

表4．6-15 圆截面轴扭转角φ的计算公式

注：d为轴的外径(mm)：d₀为空心轴的内直径(mm)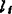；、、、分别代表阶梯轴第i段上所传递的转矩(N·mm)、长度(mm)、直径和空心轴的内直径(mm)；G为材料的剪切弹性模量，钢为。

例4．6-2 如图4．6-8所示，轴的材料为45钢，E=2．06×10⁵N／mm²，试用变形能量法求轴上C处的挠度。

图4．6-8 轴弯曲变形计算例图

解：先计算轴C处在xy平面内的挠度y_exy。求各轴段积分值的公式查表4．6-14，于是：

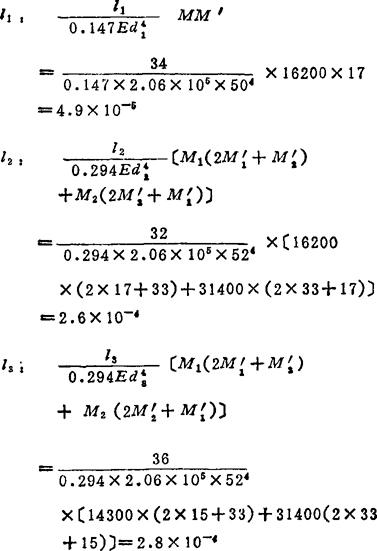
用同样的方法可求得轴C处在Z_y平面内的挠度y_cZy：

应该说明的是，这里是通过一种简单的受力情况以说明求挠度的一般方法，即分别在两个互相垂直的座标平面中求挠度，然后合成。实际上，就本例的具体情况而言，无需将齿轮所受的法向力分解。只需画出该力的弯矩图即可直接求y_c。