弹性薄板

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册上》第149页（2243字）

当构件的一个方向尺寸比其它两个方向尺寸小得多时，称为薄板或薄壳。平分薄板或薄壳厚度的面称为中面。当中面为平面时，称为薄板；当中面为曲面时，称为薄壳。机器中经常使用薄板构件，如各种容器的底板，箱体结构的壁板，以及一些设备中的加强板。

当薄板受垂直于中面的外力作用时，横截面上将产生弯矩和扭矩，引起弯曲正应力和扭转剪应力。当板的挠度与厚度之比小于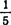时，称为小挠

度问题。在薄板小挠度弯曲理论的简化计算中，通常采用如下基本假定：

①中面法线在变形后仍为直线，且与变形后的中面垂直；

②中面内任意点不产生与中面平行的位移；

③垂直于中面方向的正应变，可以忽略不计。

等厚度平板的内力如图1．3－28所示。在横向分布载荷p(x，y)作用下，用中面挠度ω(x，y)表示的平衡方程为：

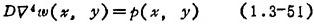
式中

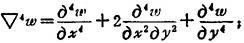
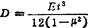，为薄板弯曲刚度，其中t为厚度，E为弹性模量，μ为泊松比。

边界条件：

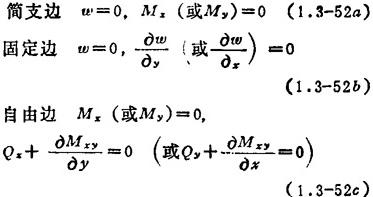
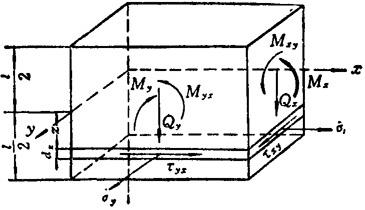
图1．3－28 平板的内力

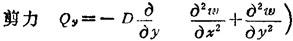
注意：薄板或薄壳的内力都是指单位宽度截面上的内力。

应力和内力的关系：

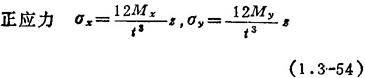
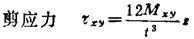
薄板的上下表面处应力最大：

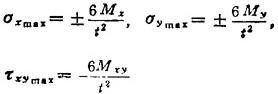
2．3．1 矩形薄板弯曲计算

表1．3－29中给出各种载荷和各种边界条件时矩形薄板的最大挠度ω_max和最大弯曲正应力σ_max计算公式。它是根据小挠度弯曲理论求得的。

表1．3－29 矩形薄板的强度和刚度计算公式

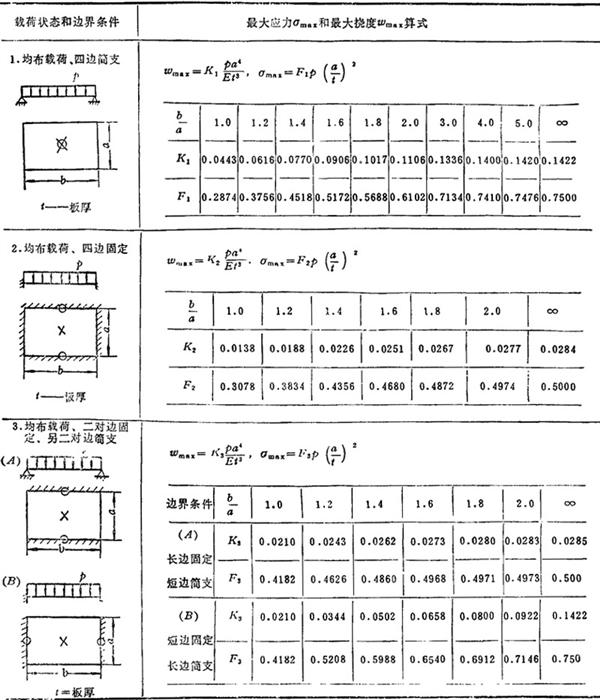
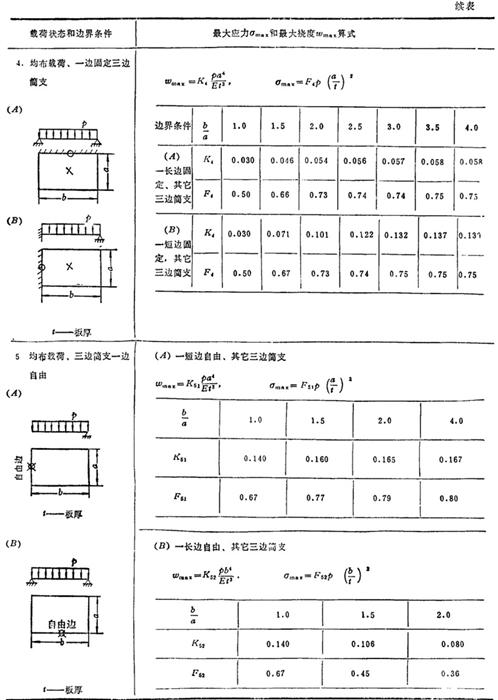
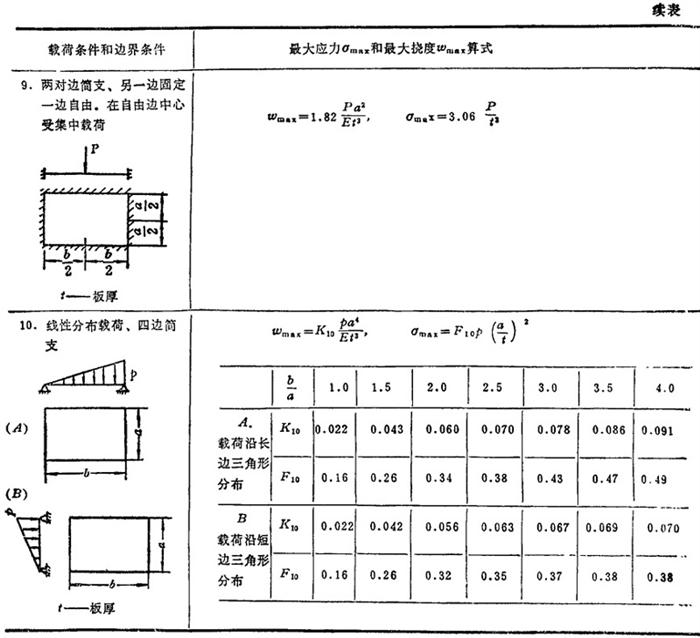
该表图中的〇标志最大弯曲正应力所在位置，×标志最大挠度所在位置。

2．3．2 圆形薄板弯曲计算

常采用极坐标求解圆形薄板的弯曲问题。极坐标系等厚薄板弯曲的平衡方程为：

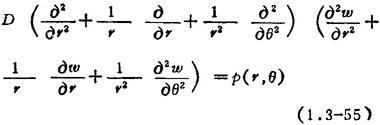
若圆板的边界条件和载荷都是轴对称的。ω不随θ而变化，则上述平衡方程又可简化为：

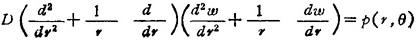
(1．3－56)

此常微分方程的解是：

ω=c₁1nr+c₂y²1nr+c₃y²+c₄+w₁(1．3－57)

其中，ω₁是一个特解，根据载荷分布形式选择。c₁、c₂、c₃、c₄是任意常数，由边界条件确定。

内力见图1．3－29，与挠度的关系有：

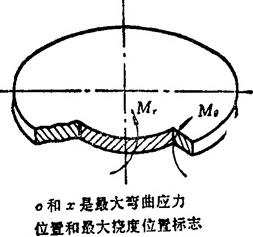
图1．3－29 圆板的内力

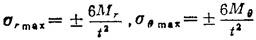
表3．1－30给出圆形薄板在各种轴对称载荷和边界条件下的挠度、板的上下表面弯曲正应力表达式及其分布规律和最大挠度和最大弯曲正应力公式。

表1．3－30 圆形薄板的强度和刚度计算公式

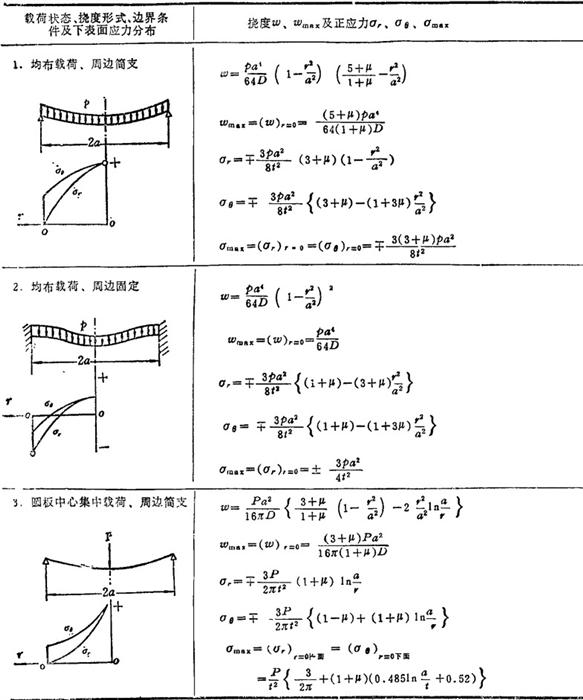
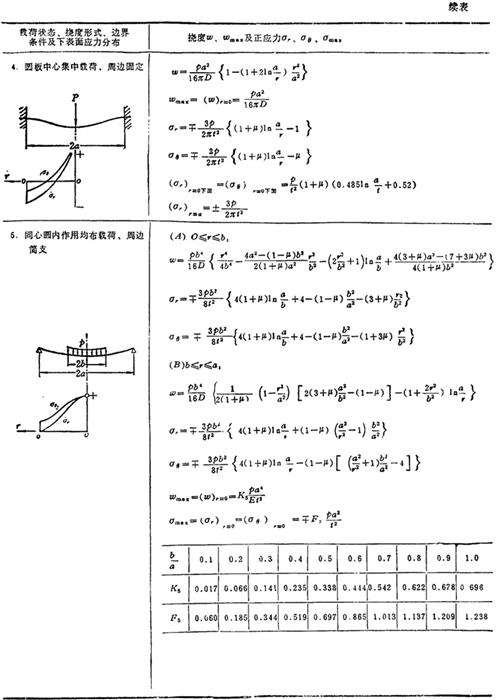
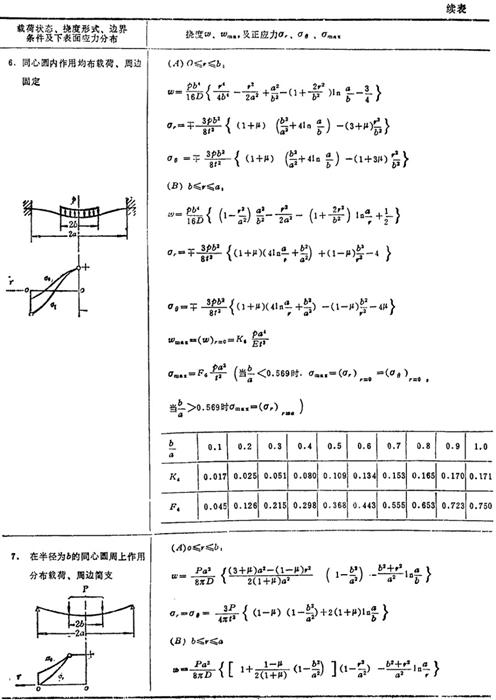
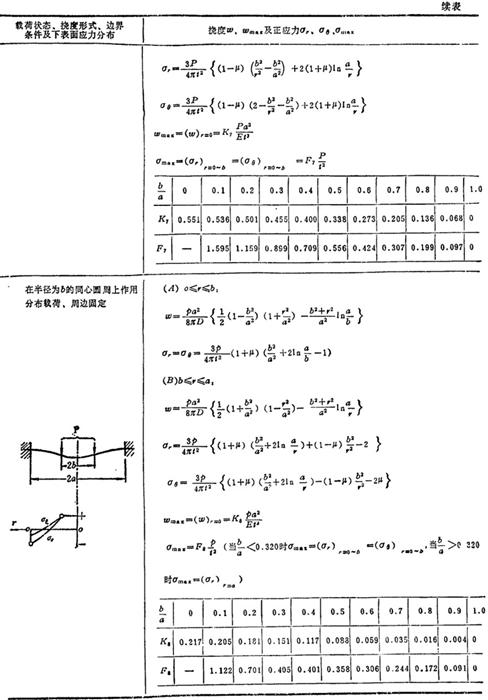
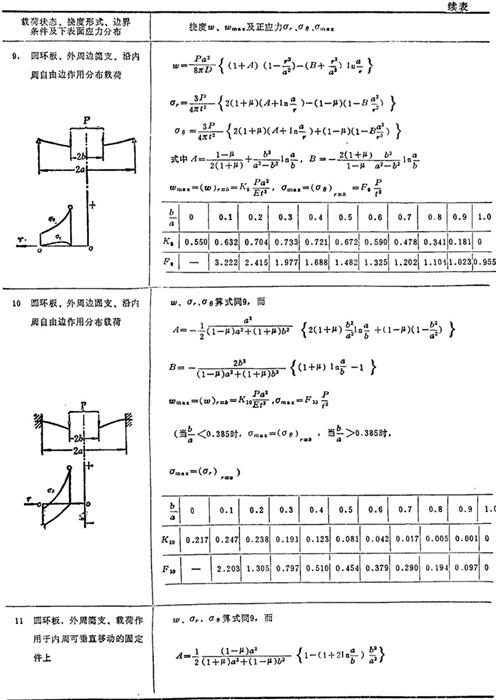
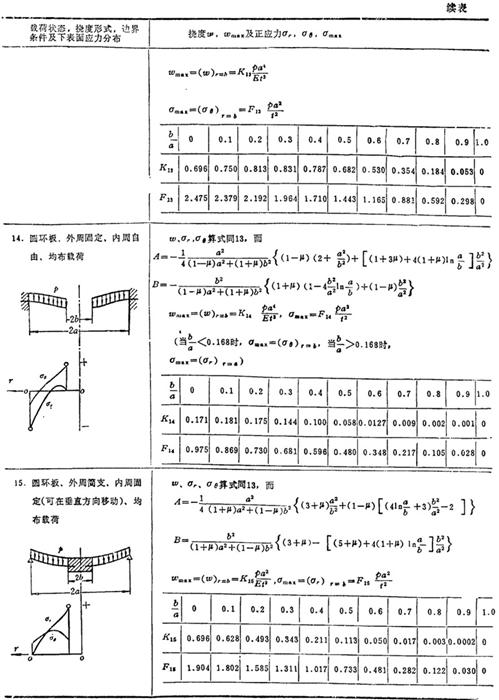
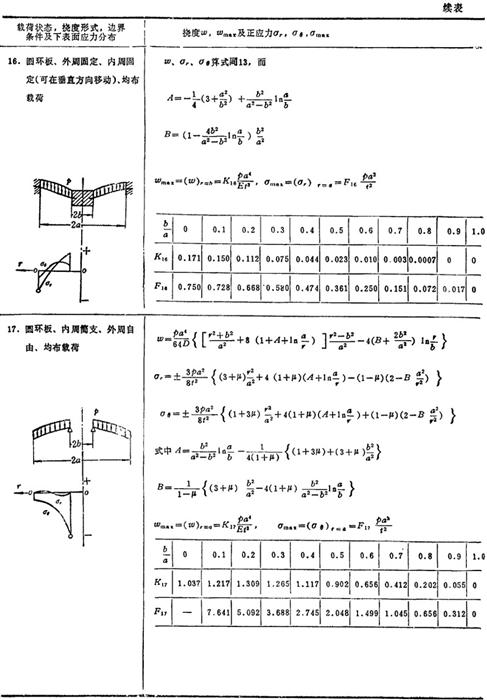
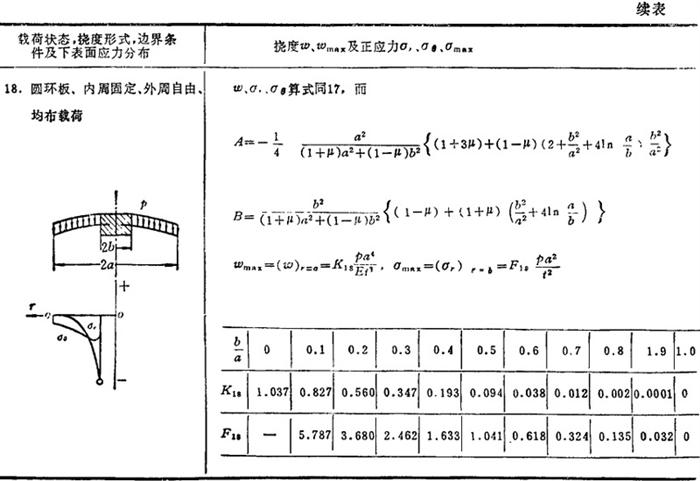
说明：p为单位面积载荷，p为集中载荷或同心圆上或周边上作用载荷的总和，t为板厚，E为弹性模量，μ为泊松比，ω_max为最大挠度，σ_max为最大弯曲正应力，a和b分别是圆板的外半径和内半径，在应力公式中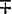符号的上面符号表示板的上表面弯曲正应力正负号，下面符号表示板的下表面弯曲正应力正负号。