工质的物性参数

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册上》第206页（2129字）

各种理想气体具有的一个共性是：在任何状态下，各种理想气体的三个基本状态参数之间都保持同一比较简单的关系式：f(p，v，T)=o。该关系式称作状态方程式。各种状态方程式的具体形式为：

对1kg气体，pv=RT (1．4－6)

式中 R为千克气体常数，J／(kg·K)。它是气体的物性参数，对不同的气体，其值是各不相同的，详见表1．4－2。

表1．4－2 气体的热力学性质

对mkg气体，则有

Pmv=mRT或PV=mRT (1．4－7)

对1kmol(千克摩尔)气体，则有

P(μv)=(μR)T (1．4－8)

μ为气体的分子量，μR=8314．3J／(kmol·K)

(1．4－9)

因为μR=8314．3J／(kmol·K)对任何理想气体都成立，故称作通用气体常数。

对nkmol气体，则更有

Pn(μv)=n(μR)T或

PV=n(μR)T (1．4－10)

除千克气体常数R外，在工程热力学中，常用的另一个物性参数是工质的比热。单位量气体温度变化1度所吸收或放出的热量称作气体的比热，用微分式表示如下：

比热的重要用途之一，就是用来计算工质的吸热量。由(1．4－11)式可得

按单位不同，比热可分为：重量比热c，单位J／(kg·K)；容积比热c^′，单位J／(Nm³·K)；千克摩尔比热μ_c，单位J／(kmol·K)。它们之间的关系是：

对同一种气体，按加热条件不同，其比热值不同，最常见的两种比热为：

定容比热 (1．4－16)

定压比热 (1．4－17)

它们之间的关系是：

cρ＞c_v，c_ρ－c_v=R_； (1．4－18)

c_p／c_ρ=K (1．4－19)

称为比热比或绝热指数。

按精确度，比热可分为如下三种：

①曲线比热

c=a₀+a₁t+a₂t²+… (1．4－22)

吸热量计算法：

或平均比热法：

各种理想气体从0℃到某温度t℃，按曲线比热所求得的平均比热值可查表1．4－3和1．4－4。

表1．4－3 气体的曲线平均定容质量比热

，kJ／(kg·K)

表1．4－4 气体的曲线平均定压质量比热

②直线比热

c=a+bt (1．4－25)

t₁与t₂间的平均比热为

0℃到某温度t之间的平均比热为

各种理想气体按直线关系所求得的值可查表1．4－5。

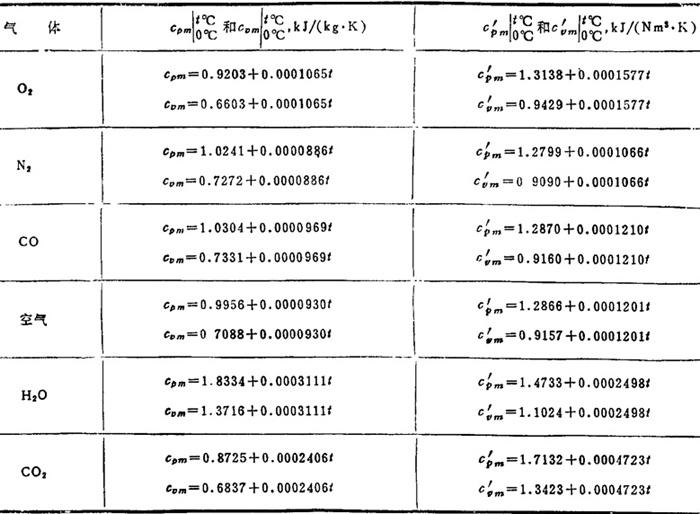
表1．4－5 气体的直线平均比热(0～1500℃适用)

如此，即可方便地求出吸热量：

③定值比热

对热力学问题进行定性分析而在精度要求不高时，可当比热值为常数，即定值比热。于是，吸热量等于

q=c(t₂－t₁)

由气体分子运动论推算出的各种原子数气体的定值千克摩尔比热的大致数值列于表1．4－6．

表1．4－6 气体定值千克摩尔比热

注：μR=8413．3J／(kmol·K)，为通用气体常数，是：此处的R应是混合气体的平均千克气体常数，改用符号R_m；而μ应为混合气体的平均分子量，改用符号μ_m。