真值表

出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第5页（1447字）

表示命题真假的表叫真值表．

(1)非p形式复合

命题真值表

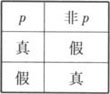
(2)p且q形式复合

命题真值表

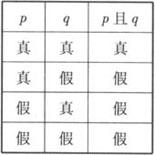
(3)p或q形式复合

命题真值表

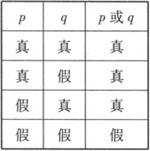
例1 分别指出下列复合命题的形式及构成它的简单命题．

(1)2既不是偶数，也不是质数；

(2)李宁是体操运动员或跳水运动员；

(3)143不是质数；

(4)正方形既是矩形，也是菱形；

(5)仅有一组对边平行的四边形是梯形或平行四边形；

(6)平行四边形不是梯形．

解 (1)这个命题是“p且q”的形式，其中p∶2不是偶数，q∶2不是质数．

(2)这是“p或q”的形式，其中p：李宁是体操运动员；q：李宁是跳水运动员．

(3)这个命题是“非p”形式，p∶143是质数．

(4)这个命题是“p且q”的形式，其中p：正方形是矩形，q：正方形是菱形．

(5)这个命题是“p或q”的形式，p：仅有一组对边平行的四边形是梯形，q：仅有一组对边平行的四边形是平行四边形．

(6)这个命题是：“非p”形式，其中p：平行四边形是梯形．

例2 分别指出下列复合命题的形式及构成它的简单命题，并判断真假．

(1)2既是偶数又是质数；

(2)0不是偶数；

(3)菱形的对角线相等或互相垂直．

解 (1)这个命题是“p且q”的形式，其中p∶2是偶数，q∶2是质数．

∵p是真命题，q也是真命题，

∴此命题(p且q)是真命题．

(2)这个题是“非p”形式，其中p∶0是偶数．

∵p是真命题，∴此命题(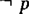)为假．

(3)这个命题是“p或q”形式，其中p：菱形的对角线相等，q：菱形的对角线互相垂直．

∵p是假命题，q为真命题，

∴此命题(p或q)为真．