一元二次方程根与系数的关系
书籍：初中数理化公式定理大全
出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《初中数理化公式定理大全》第44页（1130字）
一元二次方程ax2+bx+c=0的两个根x1，x2与系数a，b，c存在如下关系：x1+x2=－b/a，x1·x2=c/a．
注意1．一元二次方程根与系数的关系也称为韦达定理．
2．一元二次方程根与系数关系，有以下几种常见的变形形式．
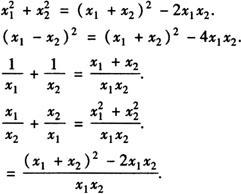
例1 已知一元二次方程x2－2x－1=0的两个根是x1，x2，则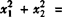
＿＿，x1－x2=＿＿．
答 6，±2
．
[解析] 由根与系数的关系，有x1+x2=2，x1·x2=－1，只要能用x1+x2，x1·x2来表示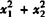
，x1－x2，就可以实现由已知向未知的转化，所以得
．
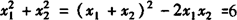(x1－x2)2=(x1+x2)2－4x1x2=8，即
．
例2 已知方程3x2+2x－11=0的两根分别为x1，x2，则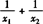
的值是( )．
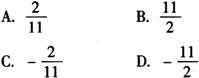
答 A．
[解析] 由根与系数关系，有
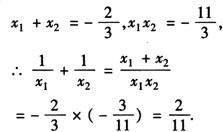
故选A．
例3 若x1，x2是一元二次方程2x2－3x+ 1=0的两个根，则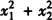
的值是＿＿．
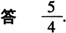
[解析] 由根与系数关系，有
例4 已知一元二次方程x2+3x+1=0的两个根x1，x2，那么(1+x1)(1+x2)的值等于＿＿．
答 －1．
[解析] 由根与系数的关系：
x1+x2=－3，x1x2=1．
∴(1+x1)(1+x2)
=1+x1+x2+x1x2
=1－3+1=－1．