相关系数
书籍:中华金融辞库
出处:按学科分类—经济 中国金融出版社《中华金融辞库》第1314页(713字)
一种对两个随机变量之间内部关联程度的测度。其计算最早由英国人KartPearson提出,故相关系数亦可称为“普尔申系数”。其计算公式:
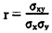
式中,r为x、y的简单相关系数;σx、σy分别为x、y的标准差;σxy为xy的协方差。
另一个英国人Spearman从“普尔申系数”出发,提出了关于两个随机变量等级变动之间的关联程度的测度公式,即等级相关系统,亦称作“Spearman系数”。其计算公式:
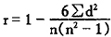
式中,r为等级相关系数;n为成对变量的个数;d为成对变量的等级之差。第三种常见的相关系数是复相关系数,在回归分析中使用。它反映被解释变量与多个解释变量之间内在关系的密切程度。一般用R表示,是拟合优度的平方根。
相关系数的数学性质:①相关系数介于-1和1之间,即,|r|≤1。②如果r>0,则两个变量呈正相关关系,即两个变量同方向变动;r<0,则两个变量呈负相关关系,即两个变量逆方向变动。③|r|=1,称为完全相关,表明两个变量之间存在确定的线性函数关系。④|r|=0,称为完全不相关,表明两个变量之间不存在任何关系,是相互独立的。⑤|r|越大则两个变量的关系越密切。一般认为,在大样本条件下,如果有|r|≥0.85,则认为两个变量之间存在强相关关系;如果0.45≤|r|≤0.85,则认为两个变量之间存在中等相关关系;如果“临界值”≤|r|≤0.45,则认为两个变量之间存在弱相关关系。