选择悖论

出处：按学科分类—政治、法律 经济科学出版社《政治经济学大辞典》第393页（1931字）

标准的选择理论把效用理论和决策理论结合起来，以明确地表达某种选择标准，在这一标准下，经济行为人可从竞争的备择方案中作出决策。

政治科学领域涉及到的选择又称为“投票”(voting)。处理投票问题的选择理论就是当前相当流行的社会选择(social choice)或公共选择(public choice)。不过，社会选择理论的起源至少可追溯到200年前的博尔达(Borda，1781)和(孔多塞Condorcet，1785)，但社会选择的正规理论却是近40年前的阿罗(Arrow，1951)和布莱克(Black，1958)提出的。

社会选择理论试图弄清楚在一定的合乎理性的要求下，人们是否能够以个人选择顺序为基础，推导出社会整体的选择顺序。

考虑一个最常见的简单多数规则。假设有3个投票人向A、B、C三个方案投票，其偏好序矩阵如下：

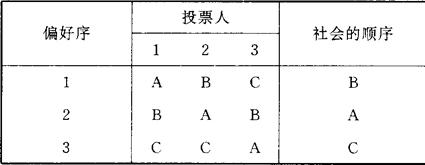
尽管B就第一偏好得票最少，从而在许多投票方式下会落选，但它有强烈的要求成为被选定的方案，因为简单多数规则下B能够击败任何一个竞争者。集体选择顺序很可能是“BPAPC”，其中P表示“多数优于”。显然，B是非占优的(Undominated)。

然而，不幸的是多数偏好关系往往不能生成社会选择顺序。一个最简单的例子如下：

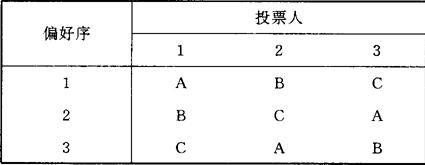
3个投票人向3个备择方案投票。由表列可知，第一个人的偏好序是：“APBPC”，第二个人的偏好序是“BPCPA”，第三个人的偏好序是“CPAPB”，应用简单多数规则投票表决，多数人认为A比B更可取(第一和第二人)；B比C更可取(第一和第二人)。这样，社会选择顺序似乎是“APBPC”。

根据“传递性”的逻辑一致性要求，必然有A比C更可取的结论。但按多数规则，C比A更可取(第二和第三人)。由此导致了循环的或矛盾的社会选择顺序：APBPCPA。这就是所谓“选择悖论”，又称为“投票悖论”、“孔多塞效应”、“阿罗问题”及“循环多数”现象等，它最初由孔多塞发现，随后交替地被遗忘和重新被发现，直到布莱克和阿罗的有关研究成果问世。

既然多数规则在选择时会产生不合理的结果，那么人们自然会去寻求其他的选择规则。比如“博尔达计数”法可使上述悖论消除。

博尔达的方法很简单，如果一共有m个备择方案，那么，在每张选票上列为第一的偏好计m分，列为第二偏好的计m－1分，依此类推，得分最多的方案被选定。上例中每个方案的“博尔达数”都是6，可以推测总体上三个方案无优劣之分，这就避免了“孔多塞效应”。

然而博尔达的方法又会产生一种悖论。考虑到上例基础上增加一个方案，个人的选择顺序矩阵如下：

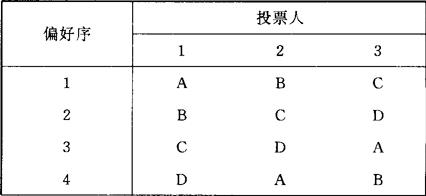
按“博尔达数”从大到小排列的社会选择顺序是：CPBPAPD。这一选择结果与上例明显不同。可见，博尔达计数法完全依赖备择方案的数目，因而与人类理性选择的要求存在明显的冲突。

各种选择规则的存在伴随着相应的悖论。换句话说，人们追求公平和平等的社会规则，同时又会创造出新的不公平、不平等。

参考文献：

Arrow，K．J．1951，Social Choice and Individual Values，New York：Wiley．

Black，D．1958，The Theory of Committees and Elections，Cambridge University Press．

Borda，J．C．1781，Memoire sur les elections au scrutin，Memoires de L’Academie Royale des Sciences，English translaton by A．de Grazia，Isia 44(1953)．

Condorcet，M．de．1785，Essai sur L’Application de L’Analyvse a Caprobabilite des Decions Rendnes a le Pluralite des Voix．Paris．